Home [Generative Model] DDIM : Denoising Diffusion Implicit Models
Post
Cancel

[Generative Model] DDIM : Denoising Diffusion Implicit Models

Posted Feb 28, 2024 Updated Mar 6, 2024
By Junyoung Kim
24 min read

해당 포스트에서는 DDIM : Denoising Diffusion Implicit Models 논문을 함께 읽어가도록 하겠습니다. 문장마다 해석을 하기 보다는 각 문단에서 중요한 부분을 요약하는 식으로 진행하겠습니다.

Emoji의 의미는 아래와 같습니다.

🔎 : 논문에 있는 내용

💡 : 논문에 적혀있지 않은 사전지식

💭 : 저의 생각

⭐ : 중요한 내용

✅ : 나중에 확인이 필요한 내용

Abstract

🔎 DDPM의 단점 : Sample을 생성하기위해 많은 step의 Markov chain 과정을 거쳐야 합니다.

🔎 DDIM : DDPM과 같은 objective function을 만드는 non-Markovian diffusion process를 통해 학습

  • 10 ~ 50배 정도 DDPM보다 빠릅니다.
  • Semantically meaningful image를 latent space에서 바로 interpolation을 통해 만들어낼 수 있습니다.
  • 매우 낮은 reconstruction error를 관찰했습니다.

1. Introduction

🔎 Generative model : GANs, VAE, Autoregressive models, normalizaing flows

🔎 그 중 GANs이 가장 좋은 품질을 만들어냈지만 학습 안정화를 하기 위해 매우 신중한 optimization과 architecture 선택이 필요합니다.

🔎 최근에는 iterative generative models에 대한 연구가 진행(DDPM, NCSN)

🔎 Iterative generative model은 GANs과 견줄만한 품질을 생성했으며 GANs에 비해 학습이 쉽다는 장점이 있습니다.

🔎 그러나 높은 품질의 sample을 생성하기 위해서는 많은 iteration이 필요해 GANs보다 매우 느리다는 단점이 있습니다.

🔎 DDPM과 GANs의 gap을 줄이기위해 DDIM을 제시합니다.

🔎 DDIM은 DDPM의 objective function과 같은 objective function을 통해 학습을 진행합니다. (Section 3)

🔎 Diffusion process에서 DDPM과 달리 non-Markovian을 사용합니다. (Section 4.1)

🔎 Reverse process는 그대로 Markov chains을 사용하는데 짧은 Markov chains 사용합니다. (Section 4.2)

🔎 DDPM보다 나은 결과 (Section 5)

  1. 더 나은 품질의 sample을 더 빠른 속도로 생성
  2. DDIM으로 생성한 sample은 consistency를 가지고 있어 똑같은 initial latent variable과 다양한 길이의 Markov chain을 통해 생성된 sample은 비슷한 feature를 가지고 있습니다.
  3. Consistency 때문에 initial latent variable을 조작해서 의미있는 이미지를 만들어낼 수 있습니다.

2. Background

💡 해당 파트는 DDPM에 있는 내용을 복습하는 부분이므로 넘어가도록 하겠습니다.

💡 다만, notation이 다른 부분이 있어 그 부분만 말씀드리고 넘어가겠습니다. (DDIM $\Longrightarrow$ DDPM)

  • $\alpha_t$ $\longrightarrow$ $\bar{\alpha}_t$
  • ELBO term을 최대화하는 $\theta$를 찾는 문제 $\longrightarrow$ Negative ELBO term을 최소화하는 $\theta$를 찾는 문제
  • $\gamma_t$ : 시간에 따른 가중치(계수) $\longrightarrow$ $\gamma_t = 1$

3. Variational Inference For Non-Markovian Forward Process

🔎 Generative model은 reverse of inference process을 approximate

  • Inference process : Diffusion process / Forward process
  • Reverse of inference process : Denoising process / Reverse process

🔎 Generative model이 image를 생성하기 위해 필요한 iteration 수를 줄이기 위해 inference process를 다시 생각할 필요가 있습니다.

🔎 DDPM의 objective인 $L_\gamma$는 marginals $q(\mathbf{x}_t|\mathbf{x}_0)$에만 의존하고 joints $q(\mathbf{x}_{1:T}|\mathbf{x}_0)$에는 직접 의존하지 않습니다.

\[\begin{align} L_\gamma(\epsilon_\theta) :=& \sum^T_{t=1}\gamma_t\mathbb{E}_{\mathbf{x}_0\sim q(\mathbf{x}_0), \epsilon_T \sim \mathcal{N}(\mathrm{0}, \mathrm{I})}\Big[ \lVert \epsilon^{(t)}_\theta {\color{Red}\mathbf{x}_t}\ -\ \epsilon_t \rVert^2_2 \Big] & \qquad \\ =& \sum^T_{t=1}\gamma_t\mathbb{E}_{\mathbf{x}_0\sim q(\mathbf{x}_0), \epsilon_T \sim \mathcal{N}(\mathrm{0}, \mathrm{I})}\Big[ \lVert \epsilon^{(t)}_\theta (\sqrt{\alpha_t}{\color{Red}\mathbf{x}_0}\ +\ \sqrt{1-\alpha_t}\epsilon_t)\ -\ \epsilon_t \rVert^2_2 \Big] & \qquad \because \mathbf{x}_t = \sqrt{\alpha_t}\mathbf{x}_0\ +\ \sqrt{1-\alpha_t}\epsilon_t \end{align}\]

🔎 같은 marginals $q(\mathbf{x}_t|\mathbf{x}_0)$을 가지는 joints $q(\mathbf{x}_{1:T}|\mathbf{x}_0)$가 많기 때문에 Non-Markovian inference process를 탐색하여 새로운 generative process로 이어지도록 합니다.

💭 $\mathbf{x}_t$를 만들 수 있는 $q(\mathbf{x}_{1:T}|\mathbf{x}_0)$는 많은데 그 중 Non-Markovian을 사용해서 특정 $\mathbf{x}_t$를 만들도록 해 새로운 generative process라 정의한다는 이야기인 것 같습니다.

🔎 새로운 generative process 또한 DDPM과 동일한 objective function을 사용할 수 있습니다.

🔎 또한 새로운 generative process를 만드는 가장 중요한 개념인 Non-Markovian이 Gaussian case를 넘어서도 적용됨을 보여주었습니다.

3.1 Non-Markovian Forward Processes

🔎 우선, inference process를 Non-Markovian으로 정의해보고자 합니다.

\[\begin{align} & q_\sigma(\mathbf{x}_{1:T}|\mathbf{x}_0) := q_\sigma(\mathbf{x}_T|\mathbf{x}_0)\prod^T_{t=2}q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) \\ & \qquad \text{where} \\ & \qquad \qquad q_\sigma(\mathbf{x}_T|\mathbf{x}_0) = \mathcal{N}(\sqrt{\alpha_T}\mathbf{x}_0, (1-\alpha_T)\mathrm{I}) \\ & \qquad \qquad q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}\big(\sqrt{\alpha_{t-1}}\mathbf{x}_0 + \sqrt{1-\alpha_{t-1} - \sigma^2_t}\cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t}\mathbf{x}_0}{\sqrt{1-\alpha_t}}, \sigma^2_t\mathrm{I}\big) \quad (t > 1) \end{align}\]

🔎 위에서 정의한 inference process가 모든 $t$에서 성립함을 귀납법을 통해 증명해야 합니다.

  1. $q_\sigma(\mathbf{x}_T|\mathbf{x}_0) = \mathcal{N}(\sqrt{\alpha_T}\mathbf{x}_0, (1-\alpha_T)\mathrm{I})$으로부터 $q_\sigma(\mathbf{x}_t|\mathbf{x}_0)$와 $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0)$을 정의

    \[\begin{align} q_\sigma(\mathbf{x}_t|\mathbf{x}_0)\ =&\ \mathcal{N}(\sqrt{\alpha_t}\mathbf{x}_0, (1-\alpha_t)\mathrm{I}) \\ q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0)\ =&\ \mathcal{N}(\sqrt{\alpha_{t-1}}\mathbf{x}_0, (1-\alpha_{t-1})\mathrm{I}) \end{align}\]

  2. $t$로부터 $t-1$를 유도할 수 있으면 모든 $t$에서 성립함을 증명

    • Bishop 2.115번 공식을 먼저 알아봐야 합니다.

      • $p(\mathbf{x})$가 Gaussian이고 $p(\mathbf{y}|\mathbf{x})$ 또한 Gaussian distribution일 때 $p(\mathbf{y})$는 Gaussian

    • Bishop 2.115번 공식과 위에서 정의한 내용을 연결 시켜보도록 하겠습니다.

      \[\begin{align} &p(\mathbf{x}) &\iff& \qquad q_{\sigma}(\mathbf{x}_t|\mathbf{x}_0)& \\ &p(\mathbf{y}|\mathbf{x}) &\iff& \qquad q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) \\ &p(\mathbf{y}) &\iff& \qquad q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0)& \\ \end{align}\]

    • 위에서 $q_{\sigma}(\mathbf{x}_t|\mathbf{x}_0)$와 $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)$를 Gaussian으로 정의했기 때문에 Bishop 2.115번 공식에 따라서 $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0)$는 Gaussian 이므로 아래와 같이 표기가 가능합니다.

      \[\begin{align} & q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0) = \mathcal{N}(\mu_{t-1}, \Sigma_{t-1}) \\ \\ & \qquad \text{where} \\ & \qquad \qquad q_\sigma(\mathbf{x}_t|\mathbf{x}_0)\ =\ \mathcal{N}(\sqrt{\alpha_t}\mathbf{x}_0, (1-\alpha_t)\mathrm{I}) \\ & \qquad \qquad q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}\big(\sqrt{\alpha_{t-1}}\mathbf{x}_0 + \sqrt{1-\alpha_{t-1} - \sigma^2_t}\cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t}\mathbf{x}_0}{\sqrt{1-\alpha_t}}, \sigma^2_t\mathrm{I}\big) \quad (t > 1) \end{align}\]

    • $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)$에 $\mathbf{x}_t$를 대입해서 $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0)$의 평균과 분산을 구합니다.

      • 위에서 정의한 $q_\sigma(\mathbf{x}_t|\mathbf{x}_0)\ =\ \mathcal{N}(\sqrt{\alpha_t}\mathbf{x}_0, (1-\alpha_t)\mathrm{I})$로 부터 reparameterization trick을 통해 $\mathbf{x}_t$를 구합니다.
      \[\begin{align} \mathbf{x}_t = \sqrt{\alpha_t}\mathbf{x}_0\ +\ \sqrt{1-\alpha_t}\epsilon_t \end{align}\]
      • $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)$에 $\mathbf{x}_t$ 대입하여 평균 파트와 분산 파트를 분리하여 계산하면 아래와 같습니다.
      \[\begin{align} \mu_{t-1} &= \sqrt{\alpha_{t-1}}\mathbf{x}_0 + \sqrt{1-\alpha_{t-1} - \sigma^2_t}\cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t}\mathbf{x}_0}{\sqrt{1-\alpha_t}} \\ &= \sqrt{\alpha_{t-1}}\mathbf{x}_0 + \sqrt{1-\alpha_{t-1} - \sigma^2_t}\cdot \frac{\sqrt{\alpha_t}\mathbf{x}_0 - \sqrt{\alpha_t}\mathbf{x}_0}{\sqrt{1-\alpha_t}} \\ &= \sqrt{\alpha_{t-1}}\mathbf{x}_0 \\ \Sigma_{t-1} &= \sigma^2_t\mathrm{I}\ +\ (1-\alpha_{t-1} - \sigma^2_t) \cdot \frac{1-\alpha_t}{1-\alpha_t} \mathrm{I} \\ &= (1-\alpha_{t-1})\mathrm{I} \end{align}\]
      • 따라서 $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0)\ =\ \mathcal{N}(\sqrt{\alpha_{t-1}}\mathbf{x}_0, (1-\alpha_{t-1})\mathrm{I})$ 입니다.

    • $t$로부터 $t-1$를 유도하였으므로 귀납법에 의해서 모든 $t$에서 성립함을 증명할 수 있었습니다.

  3. 위에서 찾은 $q_{\sigma}(\mathbf{x}_t|\mathbf{x}_0)$, $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0)$, $q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)$을 Bayes’ rule을 통해 $q_\sigma(\mathbf{x}_{t}|\mathbf{x}_{t-1}, \mathbf{x}_0)$을 구할 수 있습니다.

    \[q_\sigma(\mathbf{x}_{t}|\mathbf{x}_{t-1}, \mathbf{x}_0) = q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_0) \times \frac{q_{\sigma}(\mathbf{x}_t|\mathbf{x}_0)}{q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_0)}\]

  4. 3번에서 찾은 Bayes’ rule을 통해 inference process를 정의할 수 있습니다.

    \[q_\sigma(\mathbf{x}_{1:T}|\mathbf{x}_0) := q_\sigma(\mathbf{x}_T|\mathbf{x}_0)\prod^T_{t=2}q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)\]

🔎 DDPM의 diffusion process와 달리 DDIM의 forward process(inference process)는 더 이상 Markovian이 아닙니다.

  • 더 이상 forward process가 Markov process가 아니므로 diffusion process라고 부르지 않습니다. 따라서 Section 3에서 정리한 내용에 약간의 수정이 필요합니다.

    • Inference process : Diffusion process / Forward process
    • Reverse of inference process : Denoising process / Reverse process / Generative process

🔎 $\sigma$의 크기는 forward process가 stochastic 정도를 통제합니다.

  • $\sigma \rightarrow 0$ : 임의의 $t$에 대해 $\mathbf{x}_{0}$와 $\mathbf{x}_{t}$를 발견하는 한 하나의 $\mathbf{x}_{t-1}$를 찾을 수 있는 극단적인 경우에 도달합니다.

    💭 DDPM에서는 다양한 $\mathbf{x}_{t}$가 나타날 수 있는데 DDIM에서는 Non-Markovian을 통해 나올 수 있는 $\mathbf{x}_{t}$의 경우의 수를 조절하는 것 같습니다. 이것을 조절하는 파라미터가 $\sigma$인 것 같습니다.

    💭 그 중에서 $\sigma$가 0일 때 $\mathbf{x}_{t}$의 경우의 수를 하나로 고정하는 것 같습니다.

    💭 이처럼 $\sigma$를 조절해서 이미지를 만들어가는 과정을 reverse process 대신 generative process라 부르는 것 같습니다.

3.2 Generative Process And Unified Vairational Inference Objective

🔎 훈련 가능한 generative process $p_{\theta}(\mathbf{x}_{0:T})$에서 각 $p_{\theta}^{(t)}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$는 $q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$을 활용합니다.

🔎 $p_{\theta}^{(t)}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$를 구하는 방법을 알아보겠습니다.

  1. $\mathbf{x}_{0} \sim q(\mathbf{x}_{0})$이고 $\epsilon_{t} \sim \mathcal{N}(\mathrm{0}, \mathrm{I})$ 일 때 앞에서 정의한 식을 reparameterization trick을 활용해 $\mathbf{x}_t$를 구합니다.

    \[\mathbf{x}_t = \sqrt{\alpha_t}\mathbf{x}_0\ +\ \sqrt{1-\alpha_t}\epsilon_t \qquad \because q_{\sigma}(\mathbf{x}_t|\mathbf{x}_0) = \mathcal{N}(\sqrt{\alpha_t}\mathbf{x}_0, (1 -\alpha_t)\mathrm{I})\]

  2. 모델 $\epsilon_{\theta}^{t}(\mathbf{x}_{t})$은 $\mathbf{x}_{t}$로부터 $\epsilon_{t}$를 예측하고자 합니다.

    \[L_\gamma(\epsilon_\theta) := \sum^T_{t=1}\gamma_t\mathbb{E}_{\mathbf{x}_0\sim q(\mathbf{x}_0), \epsilon_T \sim \mathcal{N}(\mathrm{0}, \mathrm{I})}\Big[ \lVert \epsilon^{(t)}_\theta (\mathbf{x}_{t})\ -\ \epsilon_t \rVert^2_2 \Big]\]

  3. 모델 $\epsilon_{\theta}^{t}(\mathbf{x}_{t})$을 $\mathbf{x}_t = \sqrt{\alpha_t}\mathbf{x}_0\ +\ \sqrt{1-\alpha_t}\epsilon_t$에서 $\epsilon_t$ 대신 대입하고 해당 식을 $\mathbf{x}_0$으로 정리하면 아래와 같습니다.

    \[\begin{align} f_{\theta}^{(t)}(\mathbf{x}_{t}) &=\ \hat{\mathbf{x}}_0 \\ &=\ (\mathbf{x}_t - \sqrt{1-\alpha_{t}}\cdot \epsilon_{\theta}^{t}(\mathbf{x}_{t})) / \sqrt{\alpha_{t}} \end{align}\]

  4. 따라서 아래와 같이 나타낼 수 있습니다.

    \[\begin{align} q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \hat{\mathbf{x}}_{0}) &= q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, f_\theta^{(t)}(\mathbf{x}_t)) \\ &= \mathcal{N}\big(\sqrt{\alpha_{t-1}}f_{\theta}^{(t)}(\mathbf{x}_{t}) + \sqrt{1-\alpha_{t-1} - \sigma^2_t}\cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t}f_{\theta}^{(t)}(\mathbf{x}_{t})}{\sqrt{1-\alpha_t}}, \sigma^2_t\mathrm{I}\big) \end{align}\]

  5. 이제 generative process를 정의하겠습니다.

    • $p_{\theta}(\mathbf{x}_{T}) = \mathcal{N}(\mathrm{0}, \mathrm{I})$로 고정
    • Generative process가 모든 곳에서 작동하도록 하기 위해 $t=1$일 때 Gaussian noise를 추가합니다.
      • 위에서 inference process를 정의할 때 $t$가 1보다 클 때 $q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$을 정의했기 때문에 $t=1$일 때 따로 정의가 필요했음
      • $p_{\theta}^{(1)}(\mathbf{x}_{0}|\mathbf{x}_{1}) = \mathcal{N}(f_\theta^{(1)}(\mathbf{x}_1),\ \sigma_1^2\mathrm{I})$

    • 마지막으로 generative process를 정의하면 아래와 같습니다.

      \[p_{\theta}^{(t)}(\mathbf{x}_{t-1}|\mathbf{x}_{t})= \begin{cases} \mathcal{N}(f_\theta^{(1)}(\mathbf{x}_1),\ \sigma_1^2\mathrm{I}), & \text{if } t = 1 \\ q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, f_\theta^{(t)}(\mathbf{x}_t)), & \text{otherwise} \end{cases}\]

🔎 해당 논문에서는 아래와 같이 objective function을 정의했습니다.

\[\begin{align} J_{\sigma} :=& \ \mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}[\log q_\sigma(\mathbf{x}_{1:T}|\mathbf{x}_{0}) - \log p_{\theta}(\mathbf{x}_{0:T})] & \qquad \\ =&\ \mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}\Bigg[\bigg(\log q_\sigma(\mathbf{x}_T|\mathbf{x}_0)\prod^T_{t=2}q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0) \bigg) - \bigg(\log p_\theta(\mathbf{x}_T)\prod^T_{t=1}p_\theta^{(t)}(\mathbf{x}_{t-1}|\mathbf{x}_t) \bigg)\Bigg] & \qquad \\ =& \ \mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}\Bigg[ \log q_\sigma(\mathbf{x}_T|\mathbf{x}_0) + \sum^T_{t=2}\log q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x }_{0}) - \sum^T_{t=1} \log p_\theta^{(t)} (\mathbf{x}_{t-1}|\mathbf{x}_t) - \log p_\theta(\mathbf{x}_T) \Bigg] & \qquad \\ =& \ \mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}\Bigg[ \log q_\sigma(\mathbf{x}_T|\mathbf{x}_0) + \sum^T_{t=2}\log \frac{q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)}{p^{(t)}_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)} - \log p^{(1)}_\theta(\mathbf{x}_0|\mathbf{x}_1) - \log p_\theta(\mathbf{x}_T) \Bigg] & \qquad \\ \equiv& \ \mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}\Bigg[ \sum^T_{t=2}\log \frac{q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)}{p^{(t)}_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)} - \log p^{(1)}_\theta(\mathbf{x}_0|\mathbf{x}_1)\Bigg] & \qquad \because \text{학습에 필요하지 않은 부분 삭제}\\ =& \ \sum^T_{t=2}\mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}\Bigg[\log \frac{q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)}{p^{(t)}_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}\Bigg] - \mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}\big[\log p^{(1)}_\theta(\mathbf{x}_0|\mathbf{x}_1)\big] \\ =& \ \sum^T_{t=2}D_{KL}(q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)\ ||\ p^{(t)}_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)) - \mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}\big[\log p^{(1)}_\theta(\mathbf{x}_0|\mathbf{x}_1)\big] \end{align}\]

  • 위의 objective function에서 $t > 1$일 때를 살펴보겠습니다.

    \[\begin{align} D_{KL}(q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)\ ||\ p^{(t)}_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)) &= D_{KL}(q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)\ ||\ q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, f_\theta^{(t)}(\mathbf{x}_t))) & \qquad \\ &= \mathbb{E}_{\mathbf{x}_{0},\ \mathbf{x}_{t}\ \sim\ q_{\sigma}(\mathbf{x}_{0},\ \mathbf{x}_{t})} \Bigg[\frac{1}{2\sigma^2_t}\lVert \mathbf{x}_0 - f^{(t)}_\theta(\mathbf{x}_t)\rVert^2_2\Bigg] & \qquad \because \text{분산이 같은 두 Gaussian distribution} \\ &= \mathbb{E}_{\mathbf{x}_{0}\ \sim\ q_{\sigma}(\mathbf{x}_{0}),\ \epsilon\ \sim \mathcal{N}(\mathrm{0},\ \mathrm{I}),\ \mathbf{x}_t=\sqrt{\alpha_t}\mathbf{x}_0 + \sqrt{1-\alpha_t}\epsilon_t} \Bigg[\frac{1}{2\sigma^2_t}\bigg\lVert \frac{\mathbf{x}_t - \sqrt{1-\alpha_t}\epsilon_t}{\sqrt{\alpha_t}} - \frac{\mathbf{x}_t - \sqrt{1-\alpha_t}\epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\alpha_t}} \bigg\rVert^2_2 \Bigg] \\ &= \mathbb{E}_{\mathbf{x}_{0}\ \sim\ q_{\sigma}(\mathbf{x}_{0}),\ \epsilon\ \sim \mathcal{N}(\mathrm{0},\ \mathrm{I}),\ \mathbf{x}_t=\sqrt{\alpha_t}\mathbf{x}_0 + \sqrt{1-\alpha_t}\epsilon_t}\Bigg[\frac{1-\alpha_t}{2\sigma^2_t\alpha_t}\bigg\lVert \epsilon_t\ -\ \epsilon^{(t)}_\theta(\mathbf{x}_t)\bigg\rVert^2_2 \Bigg] \end{align}\]

  • 이제는 objective function에서 $t=1$일 때를 살펴보겠습니다.

    \[\begin{align} \mathbb{E}_{\mathbf{x}_{0},\ \mathbf{x}_{1}\ \sim\ q_{\sigma}(\mathbf{x}_{0},\ \mathbf{x}_{1})}\big[-\log p^{(1)}_\theta(\mathbf{x}_0|\mathbf{x}_1)\big] &\equiv \mathbb{E}_{\mathbf{x}_{0},\ \mathbf{x}_{1}\ \sim\ q_{\sigma}(\mathbf{x}_{0},\ \mathbf{x}_{1})}\Bigg[\frac{1}{2\sigma^2_1}\bigg\lVert\mathbf{x}_0 - f^{(1)}_\theta(\mathbf{x}_1) \bigg\rVert^2_2\Bigg] \\ &= \mathbb{E}_{\mathbf{x}_{0}\ \sim\ q_{\sigma}(\mathbf{x}_{0}),\ \epsilon\ \sim \mathcal{N}(\mathrm{0},\ \mathrm{I}),\ \mathbf{x}_1=\sqrt{\alpha_1}\mathbf{x}_0 + \sqrt{1-\alpha_1}\epsilon_1} \Bigg[\frac{1}{2\sigma^2_1}\bigg\lVert \frac{\mathbf{x}_1 - \sqrt{1-\alpha_1}\epsilon_1}{\sqrt{\alpha_1}} - \frac{\mathbf{x}_1 - \sqrt{1-\alpha_1}\epsilon^{(1)}_\theta(\mathbf{x}_1)}{\sqrt{\alpha_1}} \bigg\rVert^2_2 \Bigg] \\ &= \mathbb{E}_{\mathbf{x}_{0}\ \sim\ q_{\sigma}(\mathbf{x}_{0}),\ \epsilon\ \sim \mathcal{N}(\mathrm{0},\ \mathrm{I}),\ \mathbf{x}_1=\sqrt{\alpha_1}\mathbf{x}_0 + \sqrt{1-\alpha_1}\epsilon_1} \Bigg[\frac{1-\alpha_1}{2\sigma^2_1\alpha_1}\bigg\lVert \epsilon_1\ -\ \epsilon^{(1)}_\theta(\mathbf{x}_1)\bigg\rVert^2_2 \Bigg] \end{align}\]

  • 따라서 최종 objective function은 다음과 같습니다.

    \[\begin{align} J_\sigma &\equiv \sum^T_{t=2}D_{KL}(q_\sigma(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)\ ||\ p^{(t)}_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)) - \mathbb{E}_{\mathbf{x}_{0:T}\sim q_{\sigma}(\mathbf{x}_{0:T})}\big[\log p^{(1)}_\theta(\mathbf{x}_0|\mathbf{x}_1)\big] \\ &= \sum^T_{t=2}\mathbb{E}_{\mathbf{x}_{0}\ \sim\ q_{\sigma}(\mathbf{x}_{0}),\ \epsilon\ \sim \mathcal{N}(\mathrm{0},\ \mathrm{I}),\ \mathbf{x}_t=\sqrt{\alpha_t}\mathbf{x}_0 + \sqrt{1-\alpha_t}\epsilon_t}\Bigg[\frac{1-\alpha_t}{2\sigma^2_t\alpha_t}\bigg\lVert \epsilon_t\ -\ \epsilon^{(t)}_\theta(\mathbf{x}_t)\bigg\rVert^2_2 \Bigg] + \mathbb{E}_{\mathbf{x}_{0}\ \sim\ q_{\sigma}(\mathbf{x}_{0}),\ \epsilon\ \sim \mathcal{N}(\mathrm{0},\ \mathrm{I}),\ \mathbf{x}_1=\sqrt{\alpha_1}\mathbf{x}_0 + \sqrt{1-\alpha_1}\epsilon_1} \Bigg[\frac{1-\alpha_1}{2\sigma^2_1\alpha_1}\bigg\lVert \epsilon_1\ -\ \epsilon^{(1)}_\theta(\mathbf{x}_1)\bigg\rVert^2_2 \Bigg] \\ &= \sum^T_{t=1}\mathbb{E}_{\mathbf{x}_{0}\ \sim\ q_{\sigma}(\mathbf{x}_{0}),\ \epsilon\ \sim \mathcal{N}(\mathrm{0},\ \mathrm{I}),\ \mathbf{x}_t=\sqrt{\alpha_t}\mathbf{x}_0 + \sqrt{1-\alpha_t}\epsilon_t}\Bigg[\frac{1-\alpha_t}{2\sigma^2_t\alpha_t}\bigg\lVert \epsilon_t\ -\ \epsilon^{(t)}_\theta(\mathbf{x}_t)\bigg\rVert^2_2 \Bigg] \\ &= \sum^T_{t=1}\frac{1-\alpha_t}{2\sigma^2_t\alpha_t}\mathbb{E}\bigg[\big\lVert \epsilon_t\ -\ \epsilon^{(t)}_\theta(\mathbf{x}_t)\big\rVert^2_2 \bigg] \\ &= L_\gamma \qquad \text{when }\gamma_t = \frac{1-\alpha_t}{2\sigma^2_t\alpha_t} \end{align}\]

  • 최종 objective function을 생략 없이 나타낸다면 아래와 같이 나타낼 수 있습니다.

    \[J_\sigma(\epsilon_\theta) = L_\gamma(\epsilon_\theta) + C\]

4. Sampling From Generalized Generative Processes

🔎 Objective function $L_1$을 사용해서 Markov process와 Non-Markovian forward process를 학습합니다.

🔎 그렇기 때문에 pretrained DDPM을 $L_1$에 대한 해결책으로 사용할 수 있고 $\sigma$를 변경하여 새로운 generative process를 찾을 수 있습니다.

4.1 Denoising Diffusion Implicit Models

🔎 $\epsilon_{t} \sim \mathcal{N}(\mathrm{0}, \mathrm{I})$가 $\mathbf{x}_t$와 독립적이고 $\alpha_{0} := 1$이라 할 때 $\mathbf{x}_t$로부터 $\mathbf{x}_{t-1}$을 생성하는 식은 아래와 같습니다.

\[\begin{align} q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \hat{\mathbf{x}}_{0}) &= q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, f_\theta^{(t)}(\mathbf{x}_t)) & \qquad \\ &= \mathcal{N}\big(\sqrt{\alpha_{t-1}}f_{\theta}^{(t)}(\mathbf{x}_{t}) + \sqrt{1-\alpha_{t-1} - \sigma^2_t}\cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t}f_{\theta}^{(t)}(\mathbf{x}_{t})}{\sqrt{1-\alpha_t}}, \sigma^2_t\mathrm{I}\big) & \qquad \\ &= \sqrt{\alpha_{t-1}}f_{\theta}^{(t)}(\mathbf{x}_{t}) + \sqrt{1-\alpha_{t-1} - \sigma^2_t}\cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t}f_{\theta}^{(t)}(\mathbf{x}_{t})}{\sqrt{1-\alpha_t}} + \sigma_t \epsilon_t & \qquad \\ &= \sqrt{\alpha_{t-1}}\Bigg(\frac{\mathbf{x}_t - \sqrt{1-\alpha_{t}}\cdot \epsilon_{\theta}^{t}(\mathbf{x}_{t})}{\sqrt{\alpha_{t}}} \Bigg) + \sqrt{1-\alpha_{t-1} - \sigma^2_t}\cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t}\big(\frac{\mathbf{x}_t - \sqrt{1-\alpha_{t}}\cdot \epsilon_{\theta}^{t}(\mathbf{x}_{t})}{\sqrt{\alpha_{t}}} \big)}{\sqrt{1-\alpha_t}} + \sigma_t \epsilon_t & \qquad \because f_{\theta}^{(t)}(\mathbf{x}_{t}) = \frac{\mathbf{x}_t - \sqrt{1-\alpha_{t}}\cdot \epsilon_{\theta}^{t}(\mathbf{x}_{t})}{\sqrt{\alpha_{t}}}\\ &= \sqrt{\alpha_{t-1}}\underset{\text{"predicted }\mathbf{x}_{0}\text{"}}{\underbrace{\bigg(\frac{\mathbf{x}_{t} - \sqrt{1-\alpha_{t}}\epsilon^{(t)}_{\theta}(\mathbf{x}_{t})}{\sqrt{\alpha_{t}}}\bigg)}}\ +\ \underset{\text{"direction pointing to }\mathbf{x}_{t}\text{"}}{\underbrace{\sqrt{1 - \alpha_{t-1} - \sigma^{2}_{t}}\ \cdot\ \epsilon^{(t)}_{\theta}(\mathbf{x}_{t})}}\ +\ \underset{\text{random noise}}{\underbrace{\sigma_{t}\epsilon_{t}}} & \qquad \\ \end{align}\]

🔎 위에서 생각했던 것처럼 $\sigma$를 다르게 선택하면 다른 generative process가 발생하므로 모델을 다시 학습시켜야 합니다.

🔎 $\sigma_t$를 $\sqrt{(1-\alpha_{t-1})/(1-\alpha_{t})}\sqrt{1-\alpha_{t}/\alpha_{t-1}}$로 설정했을 때 forward process와 generative process는 DDPM이 됩니다.

💡 $\sigma_{t} = \sqrt{(1-\alpha_{t-1})/(1-\alpha_{t})}\sqrt{1-\alpha_{t}/\alpha_{t-1}}$은 DDPM에서 $\sigma_{t}$ 값으로 사용하는 $\tilde{\beta}_t$를 DDIM에서 사용하는 notation으로 변경한 식

🔎 $\sigma_t = 0$일 때 살펴보겠습니다.

  • $\mathbf{x}_{t-1}$과 $\mathbf{x}_{0}$가 주어졌을 때 forward process는 deterministic이 됩니다.

  • Random noise($\sigma_t\epsilon_t$)에서 $\epsilon_t$의 계수가 0이 됩니다.

  • Resulting model은 implicit probabilistic model이 되며 sample은 고정된 절차로 latent variables에서 생성됩니다.

💭 $\sigma_t = 0$으로 학습된 모델은 하나의 sample을 생성할 때 DDPM과 달리 고정된 latent를 가진다는 의미인 것 같습니다.

4.2 Accelerated Generation Processes

🔎 Denoising objective $L_1$은 $q_\sigma(\mathbf{x}_t|\mathbf{x}_0)$가 고정되어 있는 한 특정 forward procedure에 의존하지 않습니다.

💭 특정 forward procedure에 의존하지 않는 다는 것을 두 가지 측면으로 생각해 볼 수 있을 것 같습니다.

  1. $q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$을 의미적으로 생각해보기
    \[q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \hat{\mathbf{x}}_{0}) = \sqrt{\alpha_{t-1}}\underset{\text{"predicted }\mathbf{x}_{0}\text{"}}{\underbrace{f_{\theta}^{(t)}(\mathbf{x}_{t})}}\ +\ \underset{\text{"direction pointing to }\mathbf{x}_{t}\text{"}}{\underbrace{\sqrt{1 - \alpha_{t-1} - \sigma^{2}_{t}}\ \cdot\ \epsilon^{(t)}_{\theta}(\mathbf{x}_{t})}}\ +\ \underset{\text{random noise}}{\underbrace{\sigma_{t}\epsilon_{t}}}\]

    • 위의 식은 Prdicted $\mathbf{x}_0$, Direction pointing to $\mathbf{x}_t$, Random noise로 구분됩니다.

    • $\mathbf{x}_0$를 예측하고 예측된 $\mathbf{x}_0$을 $\mathbf{x}_t$의 방향으로 이동시킨 후 random noise를 추가해서 $\mathbf{x}_{t-1}$을 구한다고 생각할 수 있습니다.

    • 그렇다면 $\mathbf{x}_0$를 예측하고 $\mathbf{x}_t$를 구하기만 한다면 random noise를 조절함으로써 $\mathbf{x}_{t-1}$ 뿐만 아니라 $\mathbf{x}_{t-2}$도 구할 수 있을 것이기 때문에 denoising objective는 특정 forward procedure에 의존하지 않는다라고 할 수 있을 것 같습니다.

  2. $q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$가 어떻게 정의 되었는지 수식적으로 살펴보기

    • 이전에 $q_{\sigma}(\mathbf{x}_{t}|\mathbf{x}_{0})$가 모든 $t$에 대해서 만족함을 보일 때 $q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$가 아닌 $q_{\sigma}(\mathbf{x}_{t-2}|\mathbf{x}_{t}, \mathbf{x}_{0}) = \mathcal{N}\big(\sqrt{\alpha_{t-2}}\mathbf{x}_0 + \sqrt{1-\alpha_{t-2} - \sigma^2_t}\cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t}\mathbf{x}_0}{\sqrt{1-\alpha_t}}, \sigma^2_t\mathrm{I}\big)$라고 했을 때 $q_{\sigma}(\mathbf{x}_{t-1}|\mathbf{x}_{0})$이 아닌 $q_{\sigma}(\mathbf{x}_{t-2}|\mathbf{x}_{0})$를 구할 수 있습니다.

    • 해당 식을 subsequence에 대해 Bayes’rule로 처음 inference process(forward process)를 정의한 후 generative process를 정의하게 되면 $T$보다 짦은 subsequence 길이 만큼만으로도 sample을 만들 수 있습니다.

    • 그렇기 때문에 $q_\sigma(\mathbf{x}_t|\mathbf{x}_0)$만 변경하지 않으면 (고정되어 있으면) denoising objective는 특정 forward procedure에 의존하지 않게 됩니다.

4.3 Relevance to Neural ODEs

🔎 DDIM은 diffusion을 discrete하게 사용하기 때문에 미분 방정식이라 보긴 힘들지만 Euler’s method를 사용할 수 있는 sampling 형태를 가지고 있습니다.

  • Sampling

    \[\mathbf{x}_{t-1} = \sqrt{\alpha_{t-1}}{\bigg(\frac{\mathbf{x}_{t} - \sqrt{1-\alpha_{t}}\epsilon^{(t)}_{\theta}(\mathbf{x}_{t})}{\sqrt{\alpha_{t}}}\bigg)}\ +\ \sqrt{1 - \alpha_{t-1} - \sigma^{2}_{t}}\ \cdot\ \epsilon^{(t)}_{\theta}(\mathbf{x}_{t})\ +\ \sigma_{t}\epsilon_{t}\]

  • DDIM은 sampling 식에서 $\sigma_t = 0$으로 두어야 합니다.

    \[\begin{align} \frac{\mathbf{x}_{t-1}}{\sqrt{\alpha_{t-1}}} &= \frac{\mathbf{x}_{t} - \sqrt{1-\alpha_{t}}\epsilon^{(t)}_{\theta}(\mathbf{x}_{t})}{\sqrt{\alpha_{t}}} + \frac{\sqrt{1 - \alpha_{t-1}}\ \cdot\ \epsilon^{(t)}_{\theta}(\mathbf{x}_{t})}{\sqrt{\alpha_{t-1}}} \\ &= \frac{\mathbf{x}_{t}}{\sqrt{\alpha_{t}}} + \Bigg(\frac{\sqrt{1 - \alpha_{t-1}}}{\sqrt{\alpha_{t-1}}} - \frac{\sqrt{1-\alpha_{t}}}{\sqrt{\alpha_{t}}}\Bigg)\cdot \epsilon^{(t)}_{\theta}(\mathbf{x}_{t}) \end{align}\]

  • Discrete하기 때문에 시간 간격을 전부 $\Delta$로 바꿔줍니다.

    \[\frac{\mathbf{x}_{t - \Delta t}}{\sqrt{\alpha_{t-\Delta t}}} = \frac{\mathbf{x}_{t}}{\sqrt{\alpha_{t}}} + \Bigg(\sqrt{\frac{1-\alpha_{t-\Delta t}}{\alpha_{t-\Delta t}}} - \sqrt{\frac{1-\alpha_{t}}{\alpha_{t}}} \Bigg)\cdot \epsilon^{(t)}_{\theta}(\mathbf{x}_{t})\]

  • Euler’s method를 적용하기 위한 ODE로 만들기 위해 reparameterization을 합니다.

    \[\frac{\sqrt{1-\alpha}}{\sqrt{\alpha}} = \sigma\ , \qquad \frac{\mathbf{x}}{\sqrt{\alpha}} = \bar{\mathbf{x}}\]

  • Discrete한 sampling 식에 reaparameterization을 적용합니다.

    \[\begin{align} \frac{\mathbf{x}_{t - \Delta t}}{\sqrt{\alpha_{t-\Delta t}}}\qquad =\qquad &\frac{\mathbf{x}_{t}}{\sqrt{\alpha_{t}}} + \Bigg(\sqrt{\frac{1-\alpha_{t-\Delta t}}{\alpha_{t-\Delta t}}} - \sqrt{\frac{1-\alpha_{t}}{\alpha_{t}}} \Bigg)\cdot \epsilon^{(t)}_{\theta}(\mathbf{x}_{t}) \\ \frac{\mathbf{x}_{t - \Delta t}}{\sqrt{\alpha_{t-\Delta t}}} - \frac{\mathbf{x}_{t}}{\sqrt{\alpha_{t}}}\qquad =\qquad &\Bigg(\sqrt{\frac{1-\alpha_{t-\Delta t}}{\alpha_{t-\Delta t}}} - \sqrt{\frac{1-\alpha_{t}}{\alpha_{t}}} \Bigg)\cdot \epsilon^{(t)}_{\theta}(\mathbf{x}_{t}) \\ \mathrm{d}\bar{\mathbf{x}}(t)\qquad =\qquad &\mathrm{d}\sigma(t)\cdot \epsilon^{(t)}_{\theta}(\mathbf{x}_{t}) \\ \mathrm{d}\bar{\mathbf{x}}(t)\qquad =\qquad & \epsilon^{(t)}_{\theta}(\mathbf{x}_{t}) \mathrm{d}\sigma(t)\\ \mathrm{d}\bar{\mathbf{x}}(t)\qquad =\qquad & \epsilon^{(t)}_{\theta}\Bigg(\frac{\bar{\mathbf{x}}}{\sqrt{\sigma^2 + 1}}\Bigg) \mathrm{d}\sigma(t)\\ \end{align}\]

🔎 수정한 sampling 식은 ODE이므로 Euler’s method를 적용할 수 있습니다. 이 때 초기값은 매우 큰 $\sigma(T)$에 대하여 $\mathbf{x}(T) \sim \mathcal{N}(0, \sigma(T))$입니다.

🔎 이는 discretization step이 충분하면 $\mathbf{x}_{0}$를 $\mathbf{x}_{T}$로 인코딩 하고 위의 수정된 sampling 식의 역을 통해 디코딩 할 수 있음을 의미 합니다.

🔎 또한 $\mathbf{x}_{0}$의 인코딩 값 $\mathbf{x}_{T}$을 얻을 수 있다는 것은 모델의 latent representations를 필요로 하는 다른 downstream applications에 유용할 수 있습니다.

💭 GANs처럼 latent interpolation이 가능하지 않을까 합니다.

5. Experiments

🔎 해당 section에서는 아래의 내용들을 보여줍니다.

  1. DDPM보다 빠른 속도의 이미지 생성 (Section 5.1)
  2. DDPM과 달리 initial latent variables $\mathbf{x}_{T}$가 고정되면 DDIM은 high-level image feature를 유지 (Section 5.2)
  3. DDIM은 latent space에서 직접 interpolation (Section 5.3)
  4. Latent code로부터 reconstruction (Section 5.4)
  5. Deterministic DDIM과 stochastic DDPM 사이를 보간하는 $\tau$와 $\sigma$를 제어 (Section 5.1)

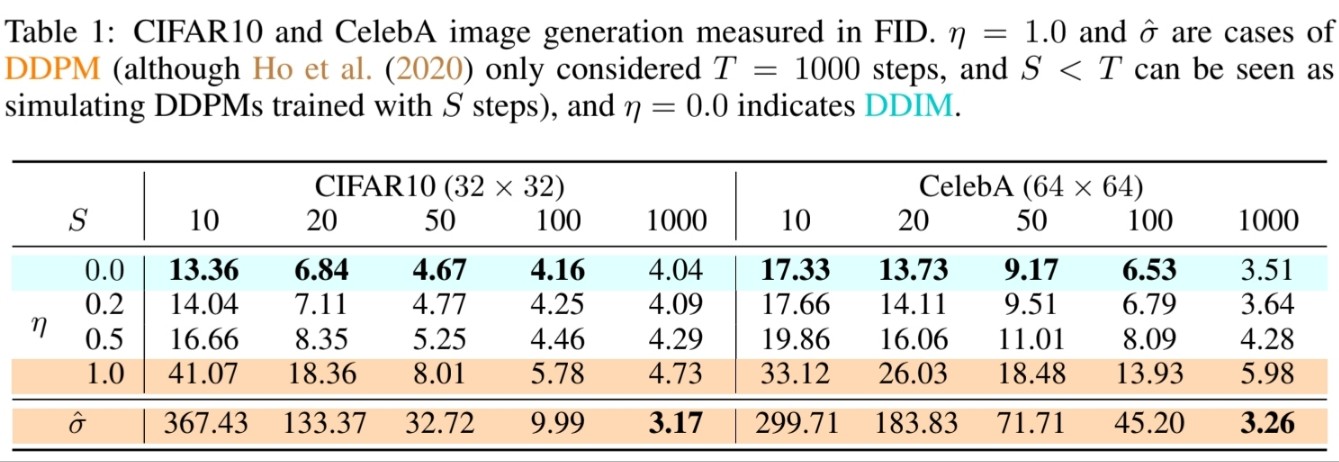
🔎 실험들의 비교를 단순화하기 위해 $\sigma$를 아래와 같이 고려합니다. 이때, $\eta$는 직접 제어가 가능한 hyperparameter이며 $\eta$를 조절해서 DDPM과 DDIM을 비교할 수 있습니다.

\[\sigma_{\tau_i}(\eta) = \eta\sqrt{(1-\alpha_{\tau_{i-1}})/(1-\alpha_{\tau_i})}\sqrt{1-\alpha_{\tau_i}/\alpha_{\tau_{i-1}}}\]

🔎 $\sigma = 1$보다 큰 standard deviation을 갖는 random noise를 사용한 DDPM을 고려합니다.

\[\hat{\sigma}:\ \hat{\sigma}_{\tau_i} = \sqrt{1-\alpha_{\tau_i}/\alpha_{\tau_{i-1}}}\]

5.1 Sample Quality And Efficiency

🔎 Sample quality는 $\text{dim}(\tau)$를 증가시킴에 따라 더 좋아집니다.

🔎 Sample Quality와 Computation cost는 반비례

🔎 DDPM의 경우 급격히 sample quality가 안좋아지는 반면 DDIM은 일관되게 좋은 sample quality를 유집합니다.

🔎 동일한 $\text{dim}(\tau)$에서 $\sigma$가 달라짐에 따라 생성된 sample을 확인할 수 있습니다.

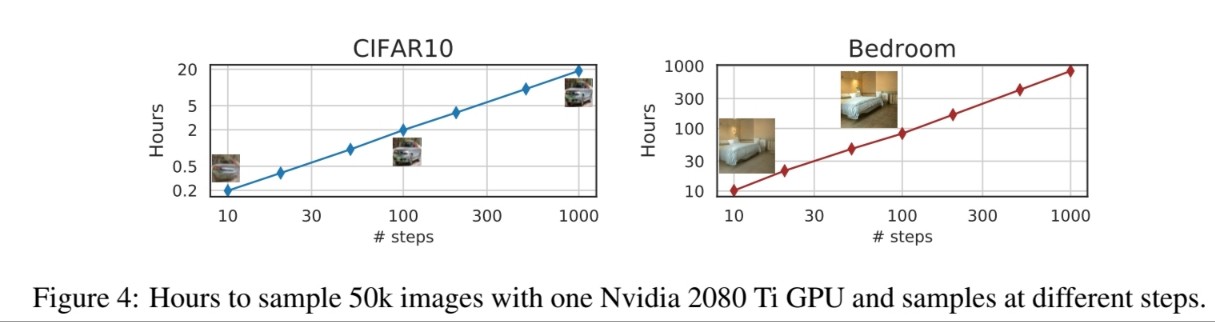
🔎 $\text{dim}(\tau)$에 따라 sample을 생성하는데 걸리는 시간이 선형적으로 증가함을 보여줍니다.

5.2 Sample Consistency In DDIMs

🔎 동일한 $\mathbf{x}_T$으로 시작하면서 서로 다른 generative trajectories($\tau$)에서 생성된 이미지를 볼 수 있습니다.

🔎 많은 경우 20 steps로 생성된 sample은 이미 1000 steps로 생성된 sample과 매우 유사하며 세부 사항에 있어서 약간의 차이만 있습니다.

🔎 따라서 $\mathbf{x}_T$만이 $\mathbf{x}_0$의 유일한 latent encoding입니다.

🔎 $\text{dim}(\tau)$이 클수록 즉, timestep이 클수록 더 좋은 sample quality를 보이지만 timestep의 길이는 high-level feature와는 상관이 없어 보입니다.

5.3 Interpolation In Detecministic Generative Processes

🔎 $\mathbf{x}_T$에 의해서 인코딩 되기 때문에 GANs과 같이 semantic interpolation이 가능해집니다.

5.4 Reconstruction From Latent Space

🔎 Reconstruction error를 계산 했을 때 DDIM은 더 큰 $S$에 대해 더 낮은 값을 가집니다.

Deep Learning, Paper Reading
Deep Learning Paper Reading Computer Vision Generative Model
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

[Generative Model] DDPM : Denoising Diffusion Probabilistic Models

[Generative Model] DDIM : Denoising Diffusion Implicit Models