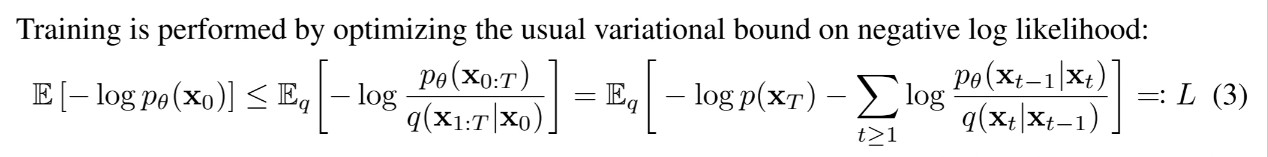Home [Generative Model] DDPM : Denoising Diffusion Probabilistic Models
Post
Cancel

[Generative Model] DDPM : Denoising Diffusion Probabilistic Models

Posted Jan 3, 2024
By Junyoung Kim
35 min read

해당 포스트에서는 DDPM : Denoising Diffusion Probabilistic Models 논문을 함께 읽어가도록 하겠습니다. 문장마다 해석을 하기 보다는 각 문단에서 중요한 부분을 요약하는 식으로 진행하겠습니다.

논문의 핵심만 알고 싶으신 분은 Paper Review으로 이동해주세요!

Emoji의 의미는 아래와 같습니다.

🔎 : 논문에 있는 내용

💡 : 논문에 적혀있지 않은 사전지식

💭 : 저의 생각

⭐ : 중요한 내용

✅ : 나중에 확인이 필요한 내용

Abstract

🔎 해당 논문은 diffusion probability models을 사용해 높은 퀄리티의 이미지를 합성했음을 보여줍니다.

💡 Diffusion probability models : Nonequilibrium thermodynamics(비평형 열역학)로부터 영감받은 latent variable models의 한 종류

💡 Latent variable models : Latent variable을 도입해 복잡한 시스템의 동작을 모델링하는 데 사용되는 통게적 모델

💡 Nonequilibrium thermodynamics : 시간에 따라 변하는 열적 및 동적 조건을 고려하는 열역학의 한 분야로, 시스템이 평형 상태가 아닐 때의 특성을 다룹니다.

🔎 Weighted variational bound에 대한 학습을 통해 가장 좋은 결과를 얻었습니다.

  • Weighted variational bound : Diffusion probability models와 denoising score matching with Langevin dynamics의 새로운 연결

    💡 Denoising score matching with Langevin dynamics : Denoising score matching을 통해 score function을 학습하고 Langevin dynamcis를 통해 sampling을 진행하는 score-based genenerative model (✅ 추후 공부 필요)

🔎 DDPM을 autoreressive decoding의 일반화로 해석될 수 있는 progressive lossy decompression 방식을 인정합니다.

1. Introduction

🔎 Generative models : GANs, Autoregressive models, flows, VAEs, Energy-based modeling, Score matching

🔎 해당 논문에서는 diffusion probabilistic models(diffusion model)의 발전을 논하고자 합니다.

🔎 Diffusion model은 유한한 시간이후에 data와 일치하는 samples을 생성하기 위해 variational inference를 사용하여 훈련된 parameterized Markov chain입니다.

💡 Variational inference : 다루기 쉬운 매개변수 $\theta$를 조정하여 확률분포 $q(\theta)$를 posteroir distribution $p(\theta|x)$에 approximation 하는 것을 말합니다.

💡 Parameterized Markov chain : Markov property를 가진 이산확률과정

💡 Markov property : 특정 상태의 확률은 오직 과거의 상태에 의존

🔎 Reverse a diffusion process(Denoising process, Transitions of markov chain)을 학습

  • Diffusion process(Forward process) : 원래의 signal(image)이 파괴될 때까지 점진적으로 data에 noise를 추가하는 markov chain
  • Diffusion process에서의 noise를 아주 작은 양의 Gaussian noise로 구성하면 denoising process 또한 conditional Gaussian으로 설정할 수 있으므로 간단한 neural network parameterization이 가능해집니다.(이전 연구에서 발견됨)

🔎 기존 diffusion model 연구의 장점과 단점

  • 장점 : Diffusion model을 정의하고 학습하기 수월

  • 단점 : High quality sample을 생성할 수 있는지 의문

🔎 DDPM에서 보여주는 diffusion model

  • ⭐ 특정 매개변수화($\epsilon$-prediction parameterization)를 통해 DDPM이 denoising score matching over multiple noise levels during training 그리고 annealed Langevin dynamics during sampling과 동등함을 보여줍니다.

  • 이러한 특정 매개변수화를 통해 high quality sample을 생성하였고 diffusion model이 아닌 다른 유형의 generative model보다 우수한 결과를 보여줬습니다.

  • 그러나 다른 log-likelihood-based model에 비해 경쟁력 있는 로그 가능성을 가지고 있지 않습니다.

    Log likelihoods : Energy based models & score matching < Diffusion model < Other likelihood-based models

  • DDPM의 lossless codelengths의 대부분이 감지할 수 없는 이미지 세부 정보를 설명하는데 사용된다는 것을 발견했습니다.

    💡 Codelengths

    • 모델이 데이터를 얼마나 효과적으로 표현하고 생성하는지를 나타내는 지표 (bits/dim)
    • 작은 codelengths는 데이터를 효과적으로 표현하는 모델임을 뜻하므로 작을수록 좋음

    💡 Lossless codelength : Lossless compresor를 통해 측정한 codelength
    💡 Lossless compresor의 대표적으로 NLL(Negativ Log Likelihood)이 있음

  • DDPM의 sampling 과정이 progressive lossy decompression 방식임을 보여줍니다.

2. Background

2.1 Reverse Process

🔎 Reverse Process : Standard normal distribution에서 학습 data로 denoising 해가는 과정이며 학습의 대상이라고 볼 수 있습니다.

\[\begin{align} p_\theta(\mathbf{x}_{0:T}) &= p_\theta(\mathbf{x}_0|\mathbf{x}_{1:T})\cdot p_\theta(\mathbf{x}_{1:T}) \tag{1} \\ &= p_\theta(\mathbf{x}_0|\mathbf{x}_{1:T})\cdot p_\theta(\mathbf{x}_1|\mathbf{x}_{2:T})\cdot p_\theta(\mathbf{x}_{2:T}) \tag{2} \\ & \qquad \vdots \\ &= p_\theta(\mathbf{x}_0|\mathbf{x}_{1:T})\cdot p_\theta(\mathbf{x}_1|\mathbf{x}_{2:T})\cdots p_\theta(\mathbf{x}_{T-1}|\mathbf{x}_T)\cdot P_\theta(\mathbf{x}_T) \tag{3} \\ &= p_\theta(\mathbf{x}_0|\mathbf{x}_1)\cdot p_\theta(\mathbf{x}_1|\mathbf{x}_2)\cdots p_\theta(\mathbf{x}_{T-1}|\mathbf{x}_T)\cdot p_\theta(\mathbf{x}_T) \tag{4} \\ &= p_\theta(\mathbf{x}_0|\mathbf{x}_1)\cdot p_\theta(\mathbf{x}_1|\mathbf{x}_2)\cdots p_\theta(\mathbf{x}_{T-1}|\mathbf{x}_T)\cdot p(\mathbf{x}_T) \tag{5} \\ &= p(\mathbf{x}_T)\cdot \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) \tag{6} \end{align}\]

2.1.1 Formula (1), (2), (3)

먼저 표기법에 대해 알아보면 $p_\theta(\mathbf{x}_{0:T})$는 매개변수 $\theta, \mathbf{x}_0, \mathbf{x}_1, \cdots, \mathbf{x}_T$의 결합확률에서 $\theta$를 고정시켰을 때의 주변확률이라고 할 수 있습니다.

아래에 기술되어 있는 공식(chain rule)을 사용하면 (1), (2), (3)을 쉽게 이해할 수 있습니다.

\[\begin{align} P(A, B, C) &= P(A \cap B \cap C) \\ &= P(A \cap (B \cap C)) \\ &= P(A | B \cap C)P(B \cap C) \\ &= P(A | B, C)P(B, C) \end{align}\]

2.1.2 Formula (4)

Reverse process는 markov property를 만족하기 때문에 markov process에 의해서 (4)처럼 (3)을 변경할 수 있습니다.

2.1.3 Formula (5)

Timestep $T$에서의 $\mathbf{x}_T$는 $\theta$와 상관없이 $\mathcal{N}(0, I)$이기 때문에 $\theta$를 지워 (5)처럼 나타낼 수 있습니다.

2.1.4 Formula (6)

(5)를 일반화 시키면 (6)으로 정리할 수 있습니다.

2.2 Forward Process (Diffusion Process)

🔎 Forward Process(Diffusion process) : Data에서 noise를 추가해 standard normal distribution으로 가는 과정입니다.

🔎 다른 유형의 latent variable models과 diffusion model의 다른 점은 noise가 Gaussian noise로 고정되어 있다는 점입니다.

\[\begin{align} q(\mathbf{x}_{1:T}|\mathbf{x}_0) &= q(\mathbf{x}_{2:T}|\mathbf{x}_0, \mathbf{x}_1)\cdot q(\mathbf{x}_1|\mathbf{x}_0) \tag{1}\\ &= q(\mathbf{x}_{3:T}|\mathbf{x}_{0:2})\cdot q(\mathbf{x}_2|\mathbf{x}_0, \mathbf{x}_1)\cdot q(\mathbf{x}_1|\mathbf{x}_0) \tag{2}\\ & \qquad \vdots \\ &= q(\mathbf{x}_T|\mathbf{x}_{0:T-1})\cdot q(\mathbf{x}_{T-1}|\mathbf{x}_{0:T-2})\cdots q(\mathbf{x}_1|\mathbf{x}_0) \tag{3}\\ &= q(\mathbf{x}_T|\mathbf{x}_{T-1})\cdot q(\mathbf{x}_{T-1}|\mathbf{x}_{T-2})\cdots q(\mathbf{x}_1|\mathbf{x}_0) \tag{4}\\ &= \prod_{t=1}^T q(\mathbf{x}_t|\mathbf{x}_{t-1}) \tag{5} \end{align}\]

2.2.1 Formula (1), (2), (3)

아래에 기술되어 있는 공식(chain rule)을 사용하면 (1), (2), (3)을 쉽게 이해할 수 있습니다.

\[\begin{align} P(A, B, C | D) &= P(A \cap B \cap C | D) \\ &= \frac{P(A \cap B \cap C \cap D)}{P(D)} \\ &= P(A \cap B | C \cap D)\cdot \frac{P(C \cap D)}{P(D)} \\ &= P(A, B | C, D)\cdot P(C | D) \\ \end{align}\]

2.2.2 Formula (4)

Forward process는 markov property를 만족하기 때문에 markov process에 의해서 (4)처럼 (3)을 변경할 수 있습니다.

2.2.3 Formula (5)

(4)를 일반화 시키면 (5)으로 정리할 수 있습니다.

2.3 Optimization Function

🔎 NLL(Negative Log Likelihood)에 대한 variational bound로 최적화를 수행합니다.

💡 Log Likelihood를 Negative Log Likelihood로 변경한 이유 : 우도를 최대화하는 문제를 최소화하는 문제로 바꾸기 위해

2.3.1 Variational Inference

  1. Variational transform

    • 비선형 함수 $f(x)$를 다루기 쉬운 선형 함수 $g(x)$로 바꾸는 것을 variational transform이라 합니다.
    • Variational transform의 한 예로 $f(x) = \log$함수를 일차함수로 변경해보겠습니다.
      • $\log$ 함수를 일차함수로 나타낸다는 것은 $\log$함수 위에 있는 모든 점을 일차함수로 표현할 수 있음을 뜻합니다.
      • $\log$ 함수의 접선은 $g(x) = \lambda x + b(\lambda)$로 나타낼 수 있을 것입니다.
      • 이 때 일차함수인 접선의 절편은 기울기 $\lambda$에 따라 달라지기 때문에 $b(\lambda)$로 표현됩니다.
      • 접점을 찾는 공식은 아래와 같이 나타낼 수 있습니다.
      \[\begin{align}y = \underset{x}{\text{min}} \{g(x) - f(x)\}\end{align}\]
      • 이제 접점 구해보겠습니다.(간단하게 $\log$함수이 밑이 $10$이라 가정)
      \[\begin{align} \frac{d}{dx} \{ g(x) - f(x) \} &=& 0 \\ \frac{d}{dx} \{ \lambda x + b(\lambda) - \ln\ x\} &=& 0 \\ \lambda - \frac{1}{x} &=& 0 \\ x &=& \frac{1}{\lambda} \end{align}\]
      • 정리를 해보면 $x = \frac{1}{\lambda}$인 모든 $x$좌표에서 $\log$ 함수를 일차함수로 표현할 수 있습니다.
    • 그러나 variationa transform에서 중요한 특징이 하나 있습니다.
    • 그것은 바로 함수가 convex하거나 concave해야만 가능합니다.

      만약 비선형 함수 $f(x)$가 convex하지 않고 concave하지도 않다면 접선 $g(x)$에는 두 개 이상의 접점이 생기기 때문입니다.

    • 이러한 특징 때문에 duality를 통해 variational tranform이 가능합니다.
      • 만약 convex하지 않거나 concave하지 않은 함수가 있다면 $\log$를 사용해 concave한 함수를 만들어 사용할 수 있습니다.
      • Deep Learning을 공부하다보면 $\log$를 사용하는 이유에는 곱을 합으로 변경해주는 이유도 있지만 concave한 특징을 사용해 variational transform하는 이유도 있다는 것을 기억하면 좋을 것 같습니다.
    • Variational transform을 정리해보면 다음과 같습니다.
      • Variational parameter $\lambda$를 도입하여 비선형 함수인 $\log$를 선형으로 변경 하는 것을 variational transform이라 할 수 있습니다.

  2. Variational Inference

    • Variational inference는 다루기 쉬운 매개변수 $\theta$를 조정하여 확률분포 $q(\theta)$를 posteroir distribution $p(\theta|x)$에 approximation 하는 것을 말합니다.
    • Variational inference의 방법으로는 KL-Divergence이 있습니다.

2.3.2 Variational Inference at DDPM

DDPM에서 variational inference가 적용되는 부분을 살펴보겠습니다.

\[\begin{align} \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p_\theta(\mathbf{x}_0)\right] &= \int(-\log\ p_\theta(\mathbf{x}_0))\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T \qquad & \\ &= \int(-\log\ \frac{p_\theta(\mathbf{x}_{0:T})}{p_\theta(\mathbf{x}_{1:T}|\mathbf{x}_0)}) \cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T \qquad & \because \text{Chain Rule} \\ &= \int(-\log\ \frac{p_\theta(\mathbf{x}_{0:T})}{p_\theta(\mathbf{x}_{1:T}|\mathbf{x}_0)} \cdot {\color{Red}\frac{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}})\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T \qquad & \\ &= \int(-\log\ \frac{p_\theta(\mathbf{x}_{0:T})}{ {\color{Red}q(\mathbf{x}_{1:T}|\mathbf{x}_0)}} \cdot \frac{ {\color{Red}q(\mathbf{x}_{1:T}|\mathbf{x}_0)}}{p_\theta(\mathbf{x}_{1:T}|\mathbf{x}_0)})\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T \qquad & \\ &= \int(-\log\ \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)})\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T + \int(-\log\ \frac{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}{p_\theta(\mathbf{x}_{1:T}|\mathbf{x}_0)})\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T \qquad & \because \log\ a\cdot b = \log\ a + \log\ b \\ &= \int(-\log\ \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)})\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T - {\color{Blue}\int(\log\ \frac{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}{p_\theta(\mathbf{x}_{1:T}|\mathbf{x}_0)})\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T} \qquad & \\ &= \int(-\log\ \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)})\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T - {\color{Blue}D_{KL}(q(\mathbf{x}_{1:T}|\mathbf{x}_0)\ ||\ p_\theta(\mathbf{x}_{1:T}|\mathbf{x}_0))} \qquad & \\ &\le \int(-\log\ \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)})\cdot q(\mathbf{x}_T|\mathbf{x}_0)\ d\mathbf{x}_T\ \qquad & \because D_{KL} \ge 0 \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}\right] \qquad & \\ &= ELBO \qquad & \\ \end{align}\]

2.3.3 Optimization Function 구하기

Section 2.1과 section 2.2를 사용해 위에서 variational inference를 통해 찾은 ELBO term을 아래와 같이 풀어 쓸 수 있습니다.

\[\begin{align} \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p_\theta(\mathbf{x}_0)\right] &\le \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ \frac{ {\color{Red}p(\mathbf{x}_{0:T})}}{ {\color{Blue}q(\mathbf{x}_{1:T}|\mathbf{x}_0)}}\right] \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ \frac{ {\color{Red}p(\mathbf{x}_T)\cdot \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}}{ {\color{Blue}\prod_{t=1}^T q(\mathbf{x}_t|\mathbf{x}_{t-1})}}\right] \qquad & \because \text{Section 2.1}\ \&\ \text{Section2.2} \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\log\prod_{t=1}^T \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t|\mathbf{x}_{t-1})}\right] \qquad & \because \log\ a\cdot b = \log\ a + \log\ b \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\left( \log\frac{p_\theta(\mathbf{x}_0|\mathbf{x}_1)}{q(\mathbf{x}_1|\mathbf{x}_0)} + \log\frac{p_\theta(\mathbf{x}_1|\mathbf{x}_2)}{q(\mathbf{x}_2|\mathbf{x}_1)} + \cdots + \log\frac{p_\theta(\mathbf{x}_{T-1}|\mathbf{x}_T)}{q(\mathbf{x}_T|\mathbf{x}_{T-1})} \right)\right] \qquad & \because \log\ a\cdot b = \log\ a + \log\ b \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=1}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t|\mathbf{x}_{t-1})}\right] \qquad & \\ &=: L \qquad & \\ \end{align}\]

지금까지 많은 공식들이 나와 헷갈릴 수 있으니 지금까지 증명했던 공식을 간단히 나타내면 아래와 같이 나타낼 수 있습니다.

\[\mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p_\theta(\mathbf{x}_0)\right] \le \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ \frac{p(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}\right] = \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=1}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t|\mathbf{x}_{t-1})}\right] =: L\]

2.4 Variance schedule $\beta_t$

🔎 $\beta_t$는 reparameterization을 통해 학습될 수 있고 hyperparameter로 두고 학습할 수 있습니다.

🔎 $\beta_t$가 매우 작을 때 diffusion process와 reverse process는 동일한 형태를 가지고 있기 때문에 reverse process의 표현성은 diffusion process의 gaussian conditionals에 의해서 부분적으로 보장됩니다. ($\because$ 이전 연구)

🔎 Diffusion process에서 주목할만 한 점은 diffusion process를 임의의 timestep $t$에서 closed form으로 나타낼 수 있다는 점입니다.

🔎 어떻게 closed form으로 나타낼 수 있는지 아래 증명과 함께 알아보겠습니다.

2.4.1 Reparameterziation Trick

딥러닝에서 필수적인 계산이라 함은 바로 chain rule에 의한 backpropagation입니다.

Backpropagation을 사용하기 위해서는 미분이 필수적인데 확률변수 $Z$는 기본적으로 미분이 불가능해 backpropagation을 할 수 없습니다.

그렇기 때문에 reparameterization trick을 사용해 미분이 가능하도록 해 backpropagation을 진행합니다.

정리를 해보면 확률변수 $Z$를 standard normal distribution에서 sampling 하는 과정이 미분 가능하도록 만들어 backpropagation을 가능하게 만드는 것이 reparameterization trick이며 아래와 같이 나타낼 수 있습니다.

\[Z \sim \mathcal{N}(\mu, \sigma^2) \Longrightarrow Z = \mu + \sigma\cdot\epsilon (\epsilon \sim \mathcal{N}(0, \mathrm{I}))\]

2.4.2 Diffusion Proecess with reprameterization trick

먼저 diffusion proecess의 time step $t$에서의 확률분포를 다시 한 번 살펴보겠습니다.

\[\begin{align} & \text{Diffusion process} : &q(\mathbf{x}_t|\mathbf{x}_{t-1}) := \mathcal{N}(\mathbf{x}_t; \sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t\mathrm{I}) \\ \\ \end{align}\]

이제 reparameterization trick을 활용해 timestep $t$에서 diffusion process를 closed form으로 나타내보도록 하겠습니다.

\[\begin{align} \mathbf{x}_t &= \sqrt{1 - \beta_t}\mathbf{x}_{t-1} + \sqrt{\beta_t}\epsilon_{t-1} (\epsilon_{t-1} \sim \mathcal{N}(0, \mathrm{I})) \qquad & \because \text{Reparameterization Trick} \\ &= \sqrt{\alpha_t}{\color{Green}\mathbf{x}_{t-1}} + \sqrt{1-\alpha_t} \epsilon_{t-1} \qquad & \because \alpha_t := 1-\beta_t \\ &= \sqrt{\alpha_t}({\color{Green}\sqrt{\alpha_{t-1}}{\mathbf{x}_{t-2} + \sqrt{1-\alpha_{t-1}} \epsilon_{t-2}}}) + \sqrt{1-\alpha_t} \epsilon_{t-1} \qquad & \\ &= \sqrt{\alpha_{t}\cdot \alpha_{t-1}}\mathbf{x}_{t-2} + {\color{Red}\sqrt{\alpha_t(1-\alpha_{t-1})}\epsilon_{t-2} + \sqrt{1-\alpha_t} \epsilon_{t-1}} \qquad & \\ &= \sqrt{\alpha_{t}\cdot \alpha_{t-1}}\mathbf{x}_{t-2} + {\color{Red}\sqrt{\alpha_t(1-\alpha_{t-1}) + 1 - \alpha_t}\bar{\epsilon}_{t-2}} \qquad & \because \epsilon_1 \sim \mathcal{N}(0, \sigma_1^2\mathrm{I})\quad \& \quad \epsilon_2 \sim \mathcal{N}(0, \sigma_2^2\mathrm{I}) \Longrightarrow \bar{\epsilon} := \epsilon_1 + \epsilon_2 \sim \mathcal{N}(0, (\sigma_1^2 + \sigma_2^2)\mathrm{I}) \\ &= \sqrt{\alpha_{t}\cdot \alpha_{t-1}}\mathbf{x}_{t-2} + {\color{Red}\sqrt{1 - \alpha_t\cdot\alpha_{t-1}}\bar{\epsilon}_{t-2}} \qquad & \\ &= \cdots \qquad & \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon \qquad & \because \bar{\alpha}_t := \alpha_t\cdot\alpha_{t-1}\cdots\alpha_1 \\ \end{align}\]

2.5 Rewriting $L$

🔎 위에서 정의한 optimization function $L$을 변경함으로써 효율적인 학습이 가능합니다.

\[\begin{align} L &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=1}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t|\mathbf{x}_{t-1})}\right] \qquad & \tag{1}\\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=2}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{\color{Orange}q(\mathbf{x}_t|\mathbf{x}_{t-1})} - \log \frac{p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)}{q(\mathbf{x}_1|\mathbf{x}_{0})}\right] \qquad & \because t = 1 \text{분리} \tag{2}\\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=2}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{\color{Orange}q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})}\cdot {\color{Orange}\frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q(\mathbf{x}_t|\mathbf{x}_{0})}} - \log \frac{p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)}{q(\mathbf{x}_1|\mathbf{x}_{0})}\right] \qquad & \because \text{Section 2.5.1} \tag{3}\\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=2}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})}-{\color{Purple}\sum_{t=2}^T\log \frac{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q(\mathbf{x}_t|\mathbf{x}_{0})}} - \log \frac{p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)}{q(\mathbf{x}_1|\mathbf{x}_{0})}\right] \qquad & \because \log\ a\cdot b = \log\ a + \log\ b \tag{4}\\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=2}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})}-\right({\color{Purple}\log \frac{q(\mathbf{x}_{1}|\mathbf{x}_{0})}{q(\mathbf{x}_{2}|\mathbf{x}_{0})} + \log \frac{q(\mathbf{x}_{2}|\mathbf{x}_{0})}{q(\mathbf{x}_{3}|\mathbf{x}_{0})} \cdots + \log \frac{q(\mathbf{x}_{T-1}|\mathbf{x}_{0})}{q(\mathbf{x}_{T}|\mathbf{x}_{0})}}\left) - \log \frac{p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)}{q(\mathbf{x}_1|\mathbf{x}_{0})}\right] \qquad & \tag{5}\\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=2}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})}-{\color{Purple}\log \frac{q(\mathbf{x}_{1}|\mathbf{x}_{0})}{q(\mathbf{x}_{T}|\mathbf{x}_{0})}} - \log \frac{p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)}{q(\mathbf{x}_1|\mathbf{x}_{0})}\right] \qquad & \because \log \frac{a}{b}+\log \frac{b}{c} = \log \frac{a}{c} \tag{6}\\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=2}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})}-\log \frac{\color{Red}q(\mathbf{x}_{1}|\mathbf{x}_{0})}{q(\mathbf{x}_{T}|\mathbf{x}_{0})} - \log \frac{p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)}{\color{Red}q(\mathbf{x}_1|\mathbf{x}_{0})}\right] \qquad & \tag{7}\\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log\ p(\mathbf{x}_T) -\sum_{t=2}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})} - \log \frac{p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)}{\color{Blue}q(\mathbf{x}_{T}|\mathbf{x}_{0})}\right] \qquad & \because \log \frac{a}{b}+\log \frac{b}{c} = \log \frac{a}{c} \tag{8}\\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log \frac{p(\mathbf{x}_T)}{\color{Blue}q(\mathbf{x}_{T}|\mathbf{x}_{0})} -\sum_{t=2}^T\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})} - \log\ p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)\right] \qquad & \tag{9}\\ &= {\color{Red}\mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log \frac{p(\mathbf{x}_T)}{q(\mathbf{x}_{T}|\mathbf{x}_{0})}\right]} + \sum_{t=2}^T{\color{Green}\mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})}\right]} + {\color{Blue}\mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[- \log\ p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)\right]} \qquad & \tag{10}\\ &= {\color{Red}D_{KL}(q(\mathbf{x}_T|\mathbf{x}_0)||p(\mathbf{x}_T))} + \sum_{t=2}^T {\color{Green}D_{KL}(q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0}) || p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t))} + {\color{Blue}\mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[- \log\ p_\theta(\mathbf{x}_{0}|\mathbf{x}_1)\right]} \qquad & \because D_{KL}(Q|P) = \mathbb{E}_{\mathbf{x}\ \sim\ Q(\mathbf{x})}\left[-\log \frac{P(\mathbf{x})}{Q(\mathbf{x})}\right] = - \sum Q(\mathbf{x})\left(\log \frac{P(\mathbf{x})}{Q(\mathbf{x})}\right) \qquad \tag{11}\\ &= {\color{Red}L_T} + \sum_{t=2}^T {\color{Green}L_{t-1}} + {\color{Blue}L_0} \qquad & \tag{12}\\ &= {\color{Red}L_T} + {\color{Green}L_{1:T-1}} + {\color{Blue}L_0} \qquad & \tag{13}\\ \end{align}\]

2.5.1 Formula (2), (3) : Rewriting $q(\mathbf{x}_t|\mathbf{x}_{t-1})$

🔎 $q(\mathbf{x}_{t}|\mathbf{x}_{t-1})$에 condition으로 $\mathbf{x}_{0}$을 추가함으로써 다루기 쉽도록 해 KL divergence(${\color{Green} L_{t-1}}$)를 통해 직접적으로 $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$와 비교할 수 있게 만들었습니다.

\[\begin{align} {\color{Orange}q(\mathbf{x}_t|\mathbf{x}_{t-1})} &= q(\mathbf{x}_t|\mathbf{x}_{t-1}, {\color{Orange}\mathbf{x}_{0}}) \qquad & \\ &= \frac{q(\mathbf{x}_t, \mathbf{x}_{t-1}, \mathbf{x}_{0})}{q(\mathbf{x}_{t-1}, \mathbf{x}_{0})} \qquad & \\ &= \frac{q(\mathbf{x}_t, \mathbf{x}_{t-1}, \mathbf{x}_{0})}{\color{Red}q(\mathbf{x}_{t-1}, \mathbf{x}_{0})}\cdot \frac{q(\mathbf{x}_t, \mathbf{x}_{0})}{\color{Purple}q(\mathbf{x}_t, \mathbf{x}_{0})} \qquad & \\ &= \frac{q(\mathbf{x}_t, \mathbf{x}_{t-1}, \mathbf{x}_{0})}{\color{Purple}q(\mathbf{x}_t, \mathbf{x}_{0})}\cdot \frac{\color{Blue}q(\mathbf{x}_t, \mathbf{x}_{0})}{\color{Red}q(\mathbf{x}_{t-1}, \mathbf{x}_{0})} \qquad & \\ &= \frac{q(\mathbf{x}_t, \mathbf{x}_{t-1}, \mathbf{x}_{0})}{q(\mathbf{x}_t, \mathbf{x}_{0})}\cdot \frac{\color{Blue}q(\mathbf{x}_t|\mathbf{x}_{0})\cdot q(\mathbf{x}_{0})}{\color{Red}q(\mathbf{x}_{t-1}|\mathbf{x}_{0})\cdot q(\mathbf{x}_{0})} \qquad & \\ &= {\color{Green}\frac{q(\mathbf{x}_t, \mathbf{x}_{t-1}, \mathbf{x}_{0})}{q(\mathbf{x}_t, \mathbf{x}_{0})}}\cdot \frac{\color{Blue}q(\mathbf{x}_t|\mathbf{x}_{0})}{\color{Red}q(\mathbf{x}_{t-1}|\mathbf{x}_{0})} \qquad & \\ &= {\color{Green}q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})}\cdot \frac{q(\mathbf{x}_t|\mathbf{x}_{0})}{q(\mathbf{x}_{t-1}|\mathbf{x}_{0})} \qquad & \\ \end{align}\]

2.6 What probability distribution $q(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$ follows

\[\begin{align} q(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) &= {\color{Red}q(\mathbf{x}_t|\mathbf{x}_{t-1})}\cdot\frac{\color{Blue}q(\mathbf{x}_{t-1}|\mathbf{x}_{0})}{\color{Green}q(\mathbf{x}_{t}|\mathbf{x}_{0})} \qquad & \because \text{Section 2.5.1}\\ &= {\color{Red}\frac{1}{\sqrt{2\pi\beta_{t}}}\exp\left(-\frac{(\mathbf{x}_{t}-\sqrt{1-\beta_{t}}\mathbf{x}_{t-1})^2}{2\beta_{t}}\right)} \cdot {\color{Blue}\frac{1}{\sqrt{2\pi(1-\bar{\alpha}_{t-1})}}\exp\left(-\frac{(\mathbf{x}_{t-1}-\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_{0})^2}{2(1-\bar{\alpha}_{t-1})}\right)} \cdot {\color{Green}\sqrt{2\pi(1-\bar{\alpha}_{t})}\exp\left(\frac{(\mathbf{x}_{t}-\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0})^2}{2(1-\bar{\alpha}_{t})}\right)}\qquad & \because x \sim \mathcal{N}(\mu, \sigma^2) \Longrightarrow f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \\ &\propto \exp\left(-\frac{(\mathbf{x}_{t}-\sqrt{1-\beta_{t}}\mathbf{x}_{t-1})^2}{2\beta_{t}}\right) \cdot \exp\left(-\frac{(\mathbf{x}_{t-1}-\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_{0})^2}{2(1-\bar{\alpha}_{t-1})}\right) \cdot \exp\left(\frac{(\mathbf{x}_{t}-\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0})^2}{2(1-\bar{\alpha}_{t})}\right) \qquad & \because \text{상수 제거} \\ &= \exp\left(-\frac{1}{2}\frac{(\mathbf{x}_{t}-\sqrt{1-\beta_{t}}{\color{Orange}\mathbf{x}_{t-1}})^2}{\beta_{t}} + \frac{({\color{Orange}\mathbf{x}_{t-1}}-\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_{0})^2}{(1-\bar{\alpha}_{t-1})} - \frac{(\mathbf{x}_{t}-\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0})^2}{(1-\bar{\alpha}_{t})}\right) \qquad & \because \exp\ a \cdot \exp\ b = \exp (a+b) \\ &= \exp\bigg(-\frac{1}{2}\Big({\color{Red}(\frac{\alpha_{t}}{\beta_{t}} + \frac{1}{1-\bar{\alpha}_{t-1}})}{\color{Orange}\mathbf{x}_{t-1}^2} - {\color{Blue} (\frac{2\sqrt{\alpha_{t}}}{\beta_{t}}\mathbf{x}_{t} + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}\mathbf{x}_{0})}{\color{Orange}\mathbf{x}_{t-1}} + C(\mathbf{x}_{t}, \mathbf{x}_{0})\Big) \bigg) \qquad & \because \text{Condition으로 }\mathbf{x}_{t}\text{와 }\mathbf{x}_{0}\text{가 주어졌을 때 }\mathbf{x}_{t-1}\text{의 확률분포를 찾고자 함} \\ &= \exp\bigg(-\frac{1}{2}\Big({\color{Red}a}\mathbf{x}_{t-1}^2 - {\color{Blue}b}\mathbf{x}_{t-1} + C(\mathbf{x}_{t}, \mathbf{x}_{0})\Big)\bigg) \qquad & \\ &= \exp\bigg(-\frac{\color{Red}a}{2}\Big(\mathbf{x}_{t-1} - \frac{\color{Blue}b}{\color{Red}a}\Big)^2 \bigg) + C^\prime(\mathbf{x}_{t}, \mathbf{x}_{0}) \qquad & \\ &\propto \frac{1}{\sqrt{2\pi\frac{1}{\color{Red}a}}}\exp\left(-\frac{(\mathbf{x}_{t-1}-\frac{\color{Blue}b}{\color{Red}a})^2}{2\frac{1}{\color{Red}a}}\right) + C^{''}(\mathbf{x}_{t}, \mathbf{x}_{0}) \qquad & \\ \end{align}\]

위의 식 $q(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$을 정리해보면 평균이 ${\color{Blue}b}/{\color{Red}a}$이고 분산이 $1/{\color{Red}a}$인 gaussian distribution임을 알 수 있습니다. 논문에 있는 식으로 정리를 해보면 아래와 같이 정리할 수 있습니다.

\[\begin{align} &q(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t-1};\tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t\mathrm{I}) \\ &\text{where}\quad \tilde{\beta} := \frac{1}{\color{Red}a} = \frac{1 - \bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot\beta_t\quad \text{and}\quad \tilde{\mu}_t(\mathbf{x}_{t}, \mathbf{x}_{0}) := {\color{Blue}b}/{\color{Red}a} = \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t \end{align}\]

🔎 결과적으로 optimization function $L$의 모든 $D_{KL}$은 gaussian distribution 비교이므로 high variance Monte Carlo estimates 대신 closed form을 사용하여 Rao-Blackwellized 방식으로 계산할 수 있습니다.

3. Diffusion models and denoising autoencoders

🔎 Diffusion models : 제약이 있는 latent variable models의 한 종류로 보일 수 있지만 구현에서 많은 자유도를 허용합니다.

Forward process(Diffusion process)의 variances $\beta_t$(Section 3.1)

Reverse process의 Gaussian distribution parameterization(Section 3.2, 3.3, 3.4)

Model Architecture(Section 4)

🔎 해당 논문의 선택을 안내하기 위해 diffusion models과 denoising score matching 사이의 새로운 연결을 확립하고 이 새로운 연결은 단순하고 가중화된 variational bound objective로 이어집니다.

🔎 DDPM은 단순성과 경험적 결과에 의해 정당화됩니다.

3.1 Forward process and $L_T$

🔎 Section 2.5에서의 $L_T$를 살펴보면 아래와 같습니다.

\[\begin{align} L_T &= D_{KL}(q(\mathbf{x}_T|\mathbf{x}_0)||p(\mathbf{x}_T)) \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log \frac{p(\mathbf{x}_T)}{q(\mathbf{x}_{T}|\mathbf{x}_{0})}\right] \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log \frac{\epsilon}{\sqrt{\bar{\alpha}_T}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_T}\epsilon}\right] \qquad & \because p(\mathbf{x}_T) = \mathcal{N}(\mathbf{x}_T; \mathrm{0}, \mathrm{I})\quad \& \quad q(\mathbf{x}_{T}|\mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_T; \sqrt{\bar{\alpha}_T}\mathbf{x}_0, (1-\bar{\alpha}_T)\mathrm{I})\\ \end{align}\]

🔎 $\beta_t$가 학습 가능한 파라미터임을 무시하고 상수로 사용합니다.

🔎 따라서 $q$는 학습 파리미터를 가지고 있지 않습니다.

⭐ 그렇기 때문에 $L_T$는 학습하지 않고 무시합니다.

3.2 Reverse process and $L_{1:T-1}$

🔎 Section 2.5에서의 $L_{t-1}$를 살펴보면 아래와 같습니다.

\[\begin{align} L_{t-1} &= D_{KL}(q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0}) || p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)) \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[-\log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_{0})}\right] \qquad & \\ \end{align}\]

3.2.1 $\Sigma_\theta(\mathbf{x}_t, t)$

🔎 먼저 $p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \Sigma_\theta(\mathbf{x}_t, t))$ for $1 < t \le T$에 대해서 논해보고자 합니다.

DDPM에서는 reverse process의 분포를 Gaussian distribution으로 설정했고 해당 분포의 평균과 분산을 $\mu_\theta(\mathbf{x}_t, t), \Sigma_\theta(\mathbf{x}_t, t)$로 정의를 했습니다.

🔎 해당 논문의 저자들은 먼저 $\Sigma_\theta(\mathbf{x}_t, t)$를 학습하지 않아도 되는 time dependent constants인 $\sigma_t^2\mathrm{I}$로 설정했습니다.

🔎 이때 실험적으로 1번 : $\sigma_t^2 = \beta_t$과 2번 : $\sigma_t^2 = \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot\beta_t \cdots 2$의 결과가 비슷함을 발견했습니다.

🔎 1번의 경우 모든 t에서 독립적이므로 $\mathbf{x}_0 \sim \mathcal{N}(\mathrm{0}, \mathrm{I})$의 경우 최적이 됩니다.

🔎 2번의 경우 이전 t에 대해서 영향을 받으므로($\bar{\alpha}_t$) 결정론적으로 한 점으로 설정된 경우 최적이 됩니다.

🔎 1번과 2번은 reverse process에 대해 각각 upper bound와 lower bound에 해당합니다.(이전 연구)

3.2.2 $\mu_\theta(\mathbf{x}_t, t)$

🔎 $\sigma_t^2 = \tilde{\beta}_t$을 활용해서 알고 있는 정보들을 정리하면 아래와 같습니다.

\[p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \sigma_t^2\mathrm{I}) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \tilde{\beta}_t\mathrm{I})\] \[q(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t-1};\tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t\mathrm{I})\]

🔎 KL-Divergence의 비교 대상인 두 분포가 분산이 같은 Gaussian distribution이므로 $L_{t - 1}$을 아래와 같이 간단하게 다시 정의할 수 있습니다.

\[\begin{align} L_{t-1} = \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\lVert\tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) - \mu_\theta(\mathbf{x}_t, t)\rVert^2\right] + C& \\ \text{where C is a constant that does not depend on }\theta& \end{align}\]

🔎 즉, $\mu_\theta$의 가장 간단한 parameterization은 forward process posterior mean인 $\tilde{\mu}_\theta$를 예측하는 모델임을 알 수 있습니다.

🔎 위에서 다시 정의한 $L_{t-1}$을 reparameterization trick을 사용해 변경하면 아래와 같습니다.

\[\begin{align} L_{1:T-1} &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\lVert\tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) - \mu_\theta(\mathbf{x}_t, t)\rVert^2\right] + C \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \because \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) = \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{ {\color{Red}\sqrt{\bar{\alpha}_{t-1}}} \beta_t}{1-\bar{\alpha}_t}\cdot\frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\epsilon}{\color{Red}\sqrt{\bar{\alpha}_t}} + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \because \mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon \Longrightarrow \mathbf{x}_0 = \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\epsilon}{\sqrt{\bar{\alpha}_t}} \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{\beta_t}{1-\bar{\alpha}_t}\cdot\frac{ {\color{Blue}\mathbf{x}_t} - \sqrt{1 - \bar{\alpha}_t}\epsilon}{\color{Red}\sqrt{\alpha_t}} + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}{\color{Blue}\mathbf{x}_t} - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\left(\frac{\beta_t}{(1-\bar{\alpha}_t) \cdot \sqrt{\alpha_t}} + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\right){\color{Blue}\mathbf{x}_t} - \frac{\beta_t\cdot {\color{Green}\sqrt{1 - \bar{\alpha}_t}}\epsilon}{ {\color{Green}(1-\bar{\alpha}_t)} \cdot \sqrt{\alpha_t}} - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\left(\frac{\beta_t}{(1-\bar{\alpha}_t) \cdot {\color{Orange}\sqrt{\alpha_t}}} + \frac{ {\color{Orange}\sqrt{\alpha_t}}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\right)\mathbf{x}_t - \frac{\beta_t\cdot\epsilon}{ {\color{Green}\sqrt{1 - \bar{\alpha}_t}} \cdot {\color{Orange}\sqrt{\alpha_t}}} - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{1}{ {\color{Orange}\sqrt{\alpha_t}}}\Bigg(\bigg(\frac{ {\color{Purple}\beta_t}}{1-\bar{\alpha}_t} + \frac{ {\color{Orange}\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\bigg)\mathbf{x}_t - \frac{\beta_t\cdot\epsilon}{ \sqrt{1 - \bar{\alpha}_t}}\Bigg) - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{1}{ \sqrt{\alpha_t}}\Bigg(\bigg(\frac{ {\color{Purple}1-\alpha_t}}{1-\bar{\alpha}_t} + \frac{ {\color{Brown}\alpha_t(1-\bar{\alpha}_{t-1})}}{1-\bar{\alpha}_t}\bigg)\mathbf{x}_t - \frac{\beta_t\cdot\epsilon}{ \sqrt{1 - \bar{\alpha}_t}}\Bigg) - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{1}{ \sqrt{\alpha_t}}\Bigg(\bigg(\frac{ 1-\alpha_t}{1-\bar{\alpha}_t} + \frac{ {\color{Brown}\alpha_t-\bar{\alpha}_{t}}}{1-\bar{\alpha}_t}\bigg)\mathbf{x}_t - \frac{\beta_t\cdot\epsilon}{ \sqrt{1 - \bar{\alpha}_t}}\Bigg) - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{1}{ \sqrt{\alpha_t}}\Bigg(\mathbf{x}_t - \frac{\beta_t}{ \sqrt{1 - \bar{\alpha}_t}}\cdot\epsilon\Bigg) - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] + C \qquad & \\ &\propto \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{1}{ \sqrt{\alpha_t}}\Bigg(\mathbf{x}_t - \frac{\beta_t}{ \sqrt{1 - \bar{\alpha}_t}}\cdot\epsilon\Bigg) - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] \qquad & \\ \end{align}\]

🔎 변경된 $L_{t-1}$에서 $\beta_t$가 상수이고 $\mathbf{x}_t$가 주어진 값이기 때문에 $\epsilon$을 예측하는 function approximator인 $\epsilon_\theta$를 통해 최소화 할 수 있습니다.

🔎 즉 아래와 같이 $L_{t-1}$을 다시 표현할 수 있습니다.

\[\begin{align} L_{t-1} &\propto \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{1}{ \sqrt{\alpha_t}}\Bigg(\mathbf{x}_t - \frac{\beta_t}{ \sqrt{1 - \bar{\alpha}_t}}\cdot\epsilon\Bigg) - \mu_\theta(\mathbf{x}_t, t)\Bigg\rVert^2\right] \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{1}{2\sigma_t^2}\Bigg\lVert\frac{1}{ \sqrt{\alpha_t}}\Bigg(\mathbf{x}_t - \frac{\beta_t}{ \sqrt{1 - \bar{\alpha}_t}}\cdot\epsilon\Bigg) - \frac{1}{ \sqrt{\alpha_t}}\Bigg(\mathbf{x}_t - \frac{\beta_t}{ \sqrt{1 - \bar{\alpha}_t}}\cdot\epsilon_\theta\Bigg)\Bigg\rVert^2\right] \qquad & \\ &= \mathbb{E}_{\mathbf{x}_T\ \sim\ q(\mathbf{x}_T|\mathbf{x}_0)}\left[\frac{\beta_t^2}{2\sigma_t^2\cdot\alpha_t\cdot(1-\bar{\alpha}_t)}\lVert\epsilon - \epsilon_\theta\rVert^2\right] \qquad & \\ \end{align}\]

🔎 이를 통해 Diffusion probability models와 denoising score matching with Langevin dynamics의 새로운 연결을 확인 할 수 있었습니다.

🔎 Sampling 절차(Algorithm 2 - denoising score mtaching)는 data density의 학습된 기울기로서 $\epsilon_\theta$을 갖는 Langevin dynamics(Variational bound for the Langevin-like reverse process)와 유사합니다.

🔎 요약하자면 reverse process mean function approximator $\mu_\theta$를 훈련하여 $\tilde{\mu}_t$를 예측할 수 있으며 $\epsilon$을 예측하도록 훈련할 수 있습니다.

🔎 $\epsilon$을 예측하도록 한 $\epsilon$-prediction parameterization이 Langevin dynamics와 유사한 것을 보여줬고 diffusion model의 variational bound를 denoising score matching과 유사한 objective로 단순화하는 것을 보여줬습니다.

🔎 그럼에도 불구하고 $p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)$의 또 다른 parameterization일 뿐이기 때문에 $\epsilon$-prediction과 $\tilde{\mu}_t$-prediction을 비교해 $\epsilon$-prediction의 효과를 Section 4에서 ablation을 통해 검증합니다.

3.3 Data scaling, reverse process decoder, and $L_0$

🔎 이미지의 구성 원소 ${0, 1, \dots, 255}$의 범위를 $[-1, 1]$로 변경함으로써 reverse process가 일관된 스케일의 입력에서 작동하도록 보장합니다.

🔎 Discrete log likelihhod를 얻기 위해 reverse process의 마지막 과정을 Gaussian distirubtion($\mathcal{N}(\mathbf{x}_{0}; \mu_\theta(\mathbf{x}_1, 1), \sigma_1^2\mathrm{I})$)에서 파생된 독립적인 discrete decoder로 설정합니다.

🔎 이러한 discrete log likelihood는 variational bound가 discrete data에 대해 lossless codelength을 보장합니다.

🔎 Sampling이 끝나면 $\mu_\theta(\mathbf{x}_1, 1)$를 noise 없이 표시합니다.

3.4 Simplified training objective

🔎 결과적으로 학습을 진행해야 하는 부분은 $L_{t-1}$과 $L_0$임을 알 수 있는데 두 objective를 합쳐 표현할 수 있습니다.

\[\begin{align} L_{\text{simple}}(\theta) &:= \mathbb{E}\left[\lVert\epsilon - \epsilon_\theta\rVert^2\right] \\ &\text{where } t \text{ is uniform between } 1 \text{and } T \end{align}\]

🔎 $t = 1$인 경우 $L_0$에 해당하고 Gaussian probability density function을 approximation하는 discrete decoder를 integral한 것으로 생각할 수 있습니다.

🔎 $t > 1$인 경우 $L_{t-1}$에서 앞의 상수를 제거한 것으로 생각할 수 있습니다.

🔎 $L_{t-1}$에서 앞의 상수를 제거하기 때문에 denoising 작업에 더 집중할 수 있도록 network를 훈련 시키는 것을 Section 4에서 실험을 통해 보여줍니다.

4. Experiments

🔎 Time step $T = 1000$

🔎 Forward process variances to constants increasing linearly ($\beta_t = 10^{-4} \sim 0.02$)

🔎 $\beta_t$는 $[-1, 1]$로 scaling된 data에 비해 상대적으로 작게 선택되어 reverse process와 forward process가 거의 동일한 기능 형태를 가지면서 signal-to-noise ratio를 가능한 작게 $\mathbf{x}_T$로 유지할 수 있습니다.

💭 Signal-to-noise ratio를 가능한 작게 $\mathbf{x}_T$로 유지한다는 것은 원래의 이미지를 찾을 수 없을 정도로 noise가 잘 추가된 것을 의미하는 것 같습니다.

🔎 U-Net backbone (similar to an unmasked PixelCNN++) with group normalization 사용

🔎 Transformer sinusoidal position embedding을 사용해서 parameter를 공유

🔎 $16 \times 16$ feature map resolution에서 self-attetion 사용

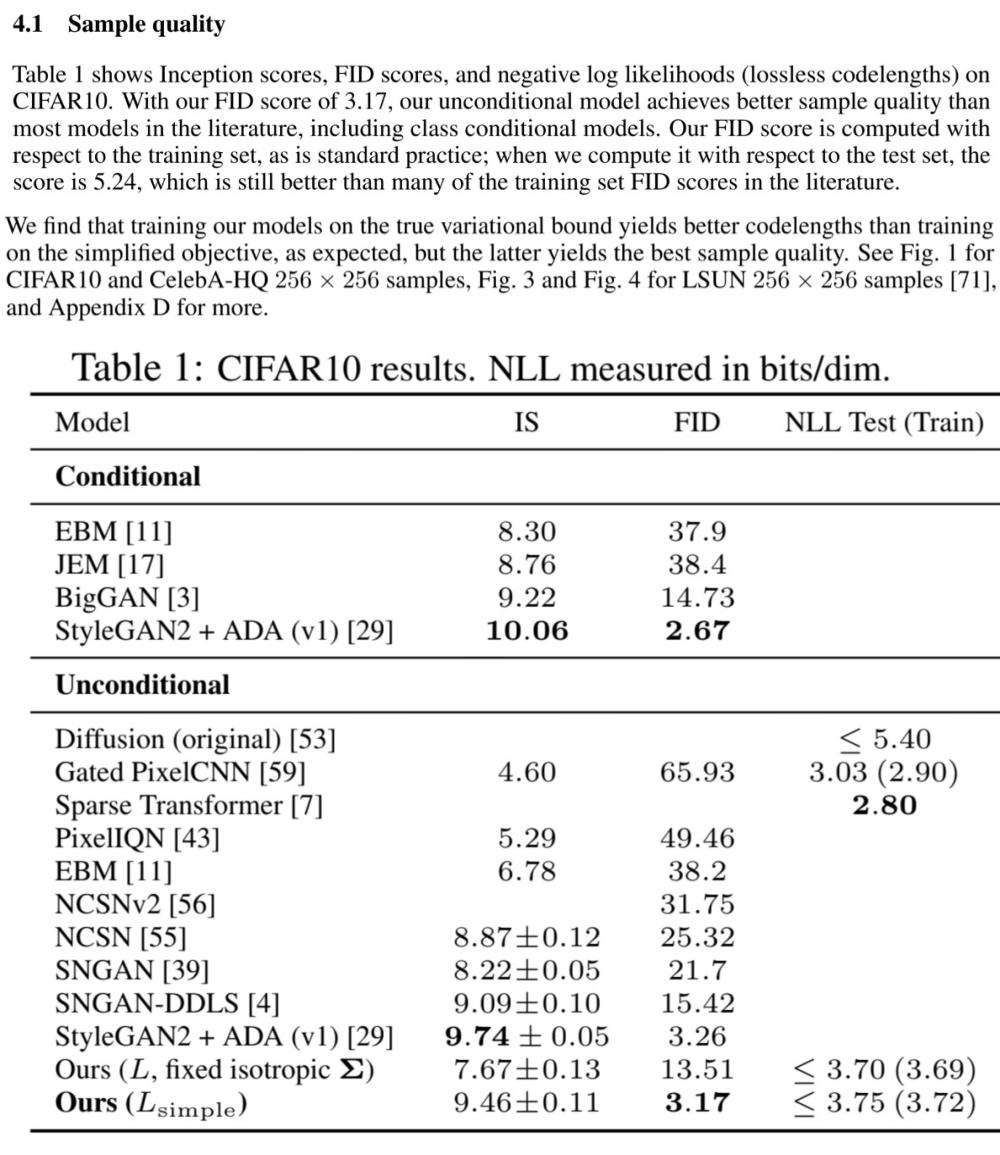
4.1 Sample quality

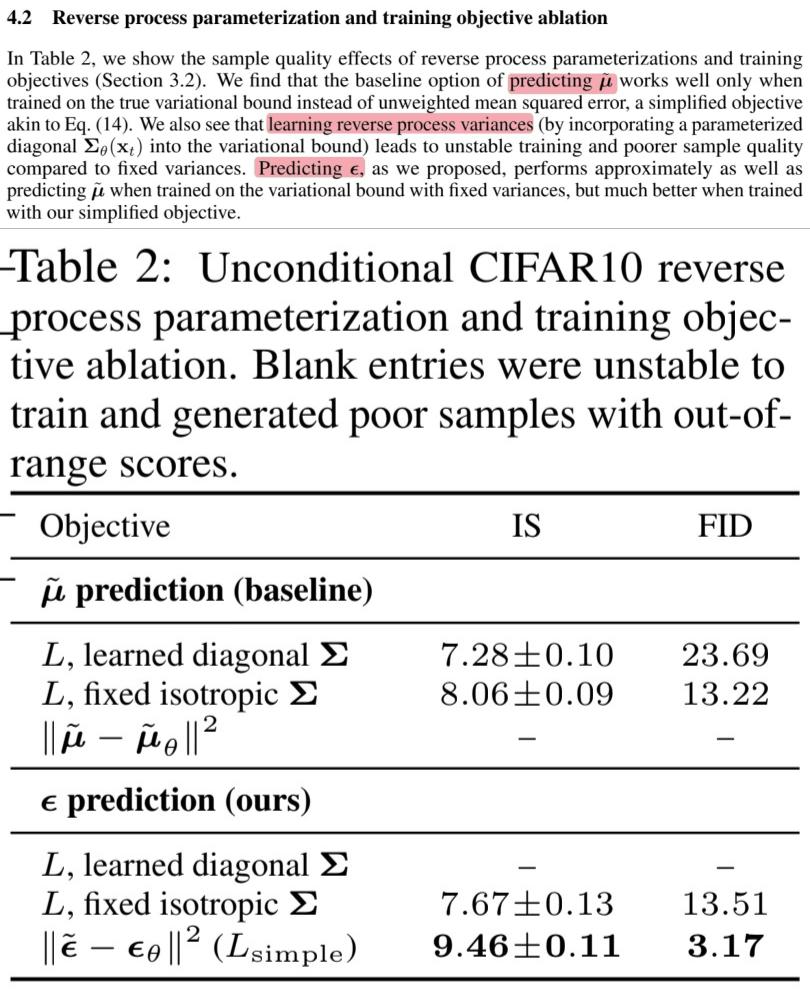
4.2 Reverse process parameterization and training objective ablation

🔎 $\tilde{\mu}$-prediction은 $L$을 단순화 하기 전에서만 잘 작동한다는 것을 발견

🔎 $\Sigma_\theta(\mathbf{x}_t, t)$를 상수로 고정시키지 않고 학습시키는 경우 학습이 불안정하며 sample quality가 저하되는 것을 알 수 있었습니다.

💡 상수로 고정 시킨 경우 notation : fixed isotropic $\Sigma$

💡 학습 대상인 경우 notation : learned diagonal $\Sigma$

🔎 $\epsilon$-prediction은 $l_{\text{simple}}$로 학습을 진행할 때 가장 좋은 결과를 얻었습니다.

4.3 Progressive coding

🔎 Train과 test 사이에 최대 $0.03$bits/dim 차이가 있지만 다른 likelihood-based model과 비슷한 차이이며 이는 diffusion model이 overfitting 되지 않았음을 알 수 있습니다.

🔎 Diffusion (original)보다는 낮은 lossless codelengths를 가지지만 다른 likelihood-based model보다는 여전히 높은 lossless codelengths를 가집니다.

🔎 그럼에도 불구하고 우리의 sample은 high quality이기 때문에 diffusion model은 훌륭한 lossy compressors를 만드는 inductive bias를 가지고 있다고 저자들은 결로 지었습니다.

🔎 $L_1 +\ \cdots\ + L_T$를 rate로, $L_0$를 distortion으로 처리하면 CIFAR10 model은 $1.78$bits/dim의 rate와 $1.97$bits/dim의 distortion을 가지며, 이는 $0$에서 $255$까지의 척도에서 $0.95$(MSE)에 해당합니다.

🔎 또한 distortion이 lossless codelengths의 절반 이상을 차지하고 있습니다.($1.97 / 3.75$)

4.3.1 Progressive lossy compression

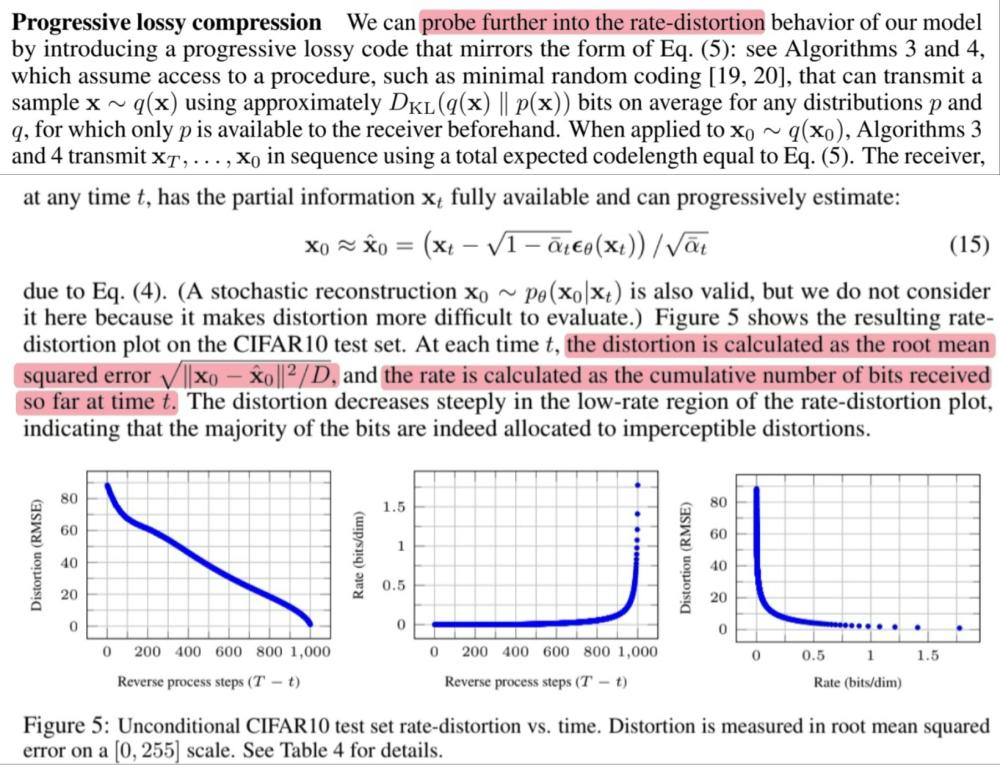
🔎 Progressive lossy code를 통해 rate-distortion에 대해 더 조사했습니다.

🔎 Receiver는 어느 $t$에서든지 부분 정보를 완전히 사용할 수 있으며 점진적으로 추정이 가능합니다.

논문의 공식 4번에서 $\mathbf{x}_0$로 식을 정리하면 아래와 같이 나타낼 수 있습니다.

$\mathbf{x}_0 \approx \hat{\mathbf{x}}_0 = (\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\epsilon) / \sqrt{\bar{\alpha}_t}$

🔎 Distortion(RMSE) : $\sqrt{\lVert\mathbf{x}_0 - \hat{\mathbf{x}}_0\rVert^2 / D}$

🔎 Rate-distortion plot에서 rate가 작은 부분에서 distortion이 매우 급격하게 줄어들었는데 이것은 비트의 대부분이 실제로 감지할 수 없는 distortion에 할당되었음을 나타냅니다.

🔎 Rate : Cumulative number of bits received so far at time $t$

4.3.2 Progressive generation

🔎 Object의 형체가 먼저 나타나고 이후 detail 정보들이 나타납니다.

🔎 이것들이 conceptual compression의 힌트일 것입니다.

4.3.3 Connection to autoregressive decoding

🔎 논문의 공식 5번의 $L_{t-1}$을 통해 Gaussian diffusion model을 좌표 순서를 reordering한 일종의 autoregressive model로 해석할 수 있습니다.

🔎 Noise를 이미지에 추가할 때 Gaussian noise가 masking noise보다 자연스럽기 때문에 더 나은 효과를 보인 것 같습니다.

🔎 또한 Gaussian diffusion length는 데이터 차원과 동일하지 않아도 되므로 빠른 sampling을 위해 더 짧게 또는 모델 표현성을 위해 더 길게 만들 수 있습니다.

💭 Autoregressive model의 경우 데이터 차원과 동일할 수 밖에 없기 때문에 Gaussian diffusion의 장점을 말하는 것으로 보입니다.

4.4 Interpolation

🔎 Image space : $\mathbf{x}_0, \mathbf{x}_0^\prime \sim q(\mathbf{x}_0)$

🔎 Diffused space : $\mathbf{x}_t, \mathbf{x}_t^\prime \sim q(\mathbf{x}_t|\mathbf{x}_0)$

🔎 Linearly interpolated latent : $\bar{\mathbf{x}}_t = (1-\lambda)\mathbf{x}_0 + \lambda\mathbf{x}_0^\prime$

🔎 Reverse process를 통해 image space로 보낸 결과 (최종 결과) : $\bar{\mathbf{x}}_0 \sim p(\mathbf{x}_0|\bar{\mathbf{x}}_t)$

Deep Learning, Paper Reading
Deep Learning Paper Reading Computer Vision Generative Model
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

[Generative Model] CycleGAN : Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

[Generative Model] DDPM : Denoising Diffusion Probabilistic Models