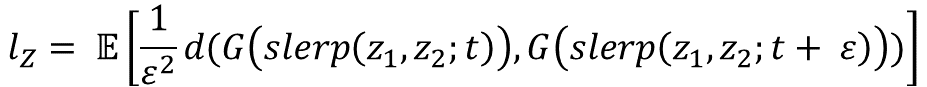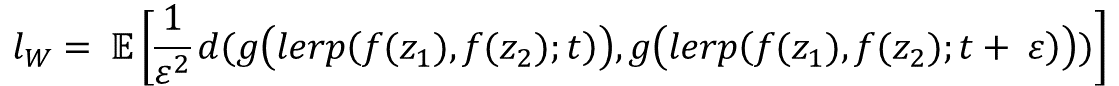[Generative Model] StyleGAN : A Style-Based Generator Architecture for Generative Adversarial Networks

이번에 리뷰할 논문은 2019년 CVPR에 발표된 “A Style-Based Generator Architecture for Generative Adversarial Networks”입니다.

---

1. Introduction

기존에 존재하던 GAN에 대한 고찰을 통해 해당 논문에서는 어떠한 점을 개선하였는지 알 수 있었습니다.

1.1 해당 논문 이전 GAN(Generative Adversarial Network)에 대한 고찰

• Generator는 black boxes이다.

  • Black Box → Generator가 정확히 어떻게 작동하는지 알 수 없는 상태를 뜻한다.

• 최근에 많은 노력에도 불구하고 Image Synthesis Process의 다양한 측면에 대한 이해가 여전히 부족하다.

• Properties of the latent space 또한 잘 이해되지 않는다.

  • 일반적으로 입증된 latent space interpolation은 서로 다른 generator를 비교하는 quantitative way를 제공하지 않는다.

1.2 Generator Architectur를 재설계

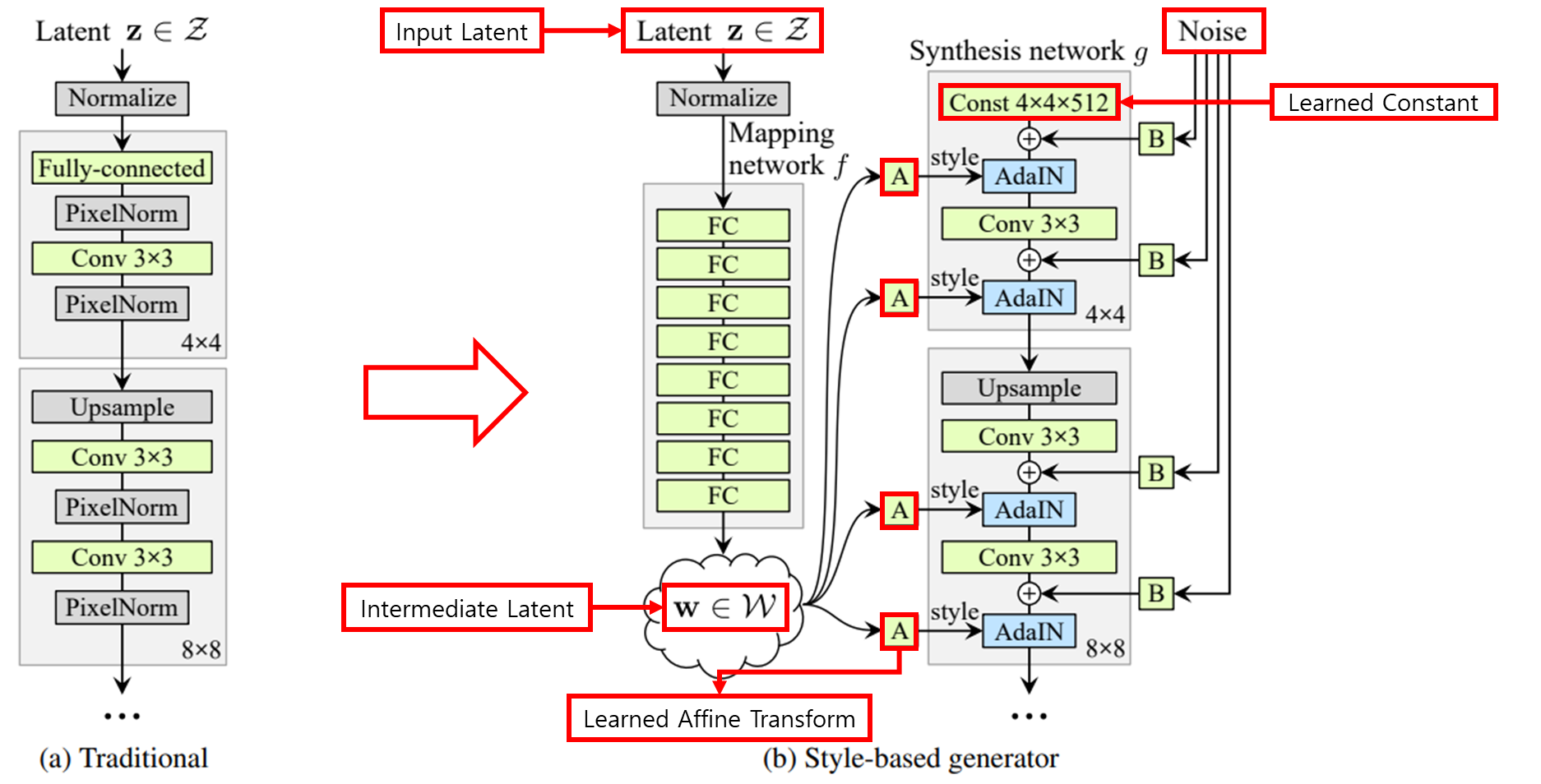
• Traditional Generator
  • Latent z가 input으로 직접 들어가는 것을 알 수 있다.
• Style-based Generator → 재설계된 generator
  • Latent z를 mapping network $f$에 input으로 넣어 latent w를 얻는다.
  • 얻은 latent w를 기반으로 synthesis network $g$의 각 convolution layer에서 style을 조정함으로써 서로 다른 scale의 features를 제어할 수 있다.
  • Syntehsis network $g$에서 convolution 연산을 하기 위해서는 input이 있어야 하는데 해당 input으로 latent z를 넣게 되면 mapping network $f$를 설계한 이유가 사라지므로 latent z를 대신해서 4 x 4 x 512의 convolution layer를 input으로 하고 학습이 가능하도록 한다.
  • 위와 같은 architecture 변경과 더불어 Network에 noise를 직접 넣어줌으로써 다음을 가능하게 한다.
    • Stochastic variation(freckles, hair)으로부터 high-level attributes(pose, identity)를 자동으로 분리
    • intuitive scale-specific mixing과 interpolation operation을 가능하게 한다.

1.3 Latent Code

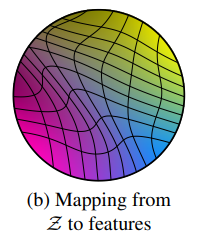
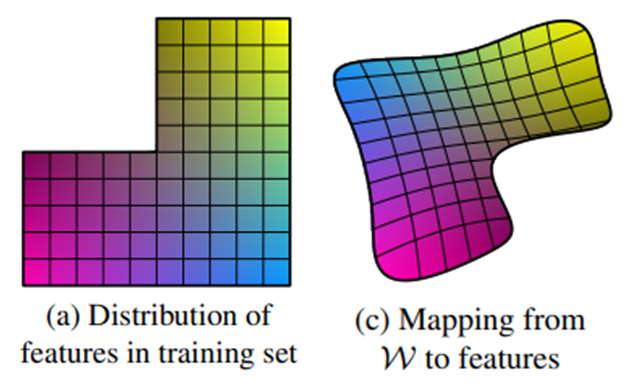
• Latent z는 training data의 probability density를 따라야 하므로 entangle 할 수 밖에 없다.

• 그러나 Latent w는 training data의 probability density를 따르지 않아도 되므로 disentangle 할 수 있다.

• Mapping Network는 entangle한 latent code를 disentangle 하도록 학습이 되어야 하며 이는 variation factor를 어떻게 표현할지를 network가 학습해야 하는 것을 의미한다.

• 학습을 위해서는 정량화가 필요한데 latent space의 disentanglement를 측정하는 이전의 방법들을 새로운 architecture에 적용할 수 없기 때문에 새로운 architecture에 맞는 두 가지 새로운 방법을 제안했다. → perceptual path length & linear sepability

• 새로운 방법 두가지를 통해 variation factor가 더욱 선형적이고 distanglement하도록 학습이 되었음을 해당 논문에서 확인할 수 있다.

• Entangle → 서로 얽혀 있는 상태여서 특징 구분이 어려운 상태를 뜻한다.

• Disentangle → Variation factor가 잘 구분 되어 있는 상태여서 선형적으로 factor를 변경했을 때 결과물들이 선형적으로 변화하는 상태

1.4 FFHQ (Flickr-Faces-HQ)

• 기존 고해상도 dataset보다 훨씬 높은 품질을 제공하고 상당히 광범위한 변형을 다루는 새로운 human faces dataset을 제시했다.

---

2. Style-based generator

Generator를 어떻게 재설계 했는지 확인할 수 있다.

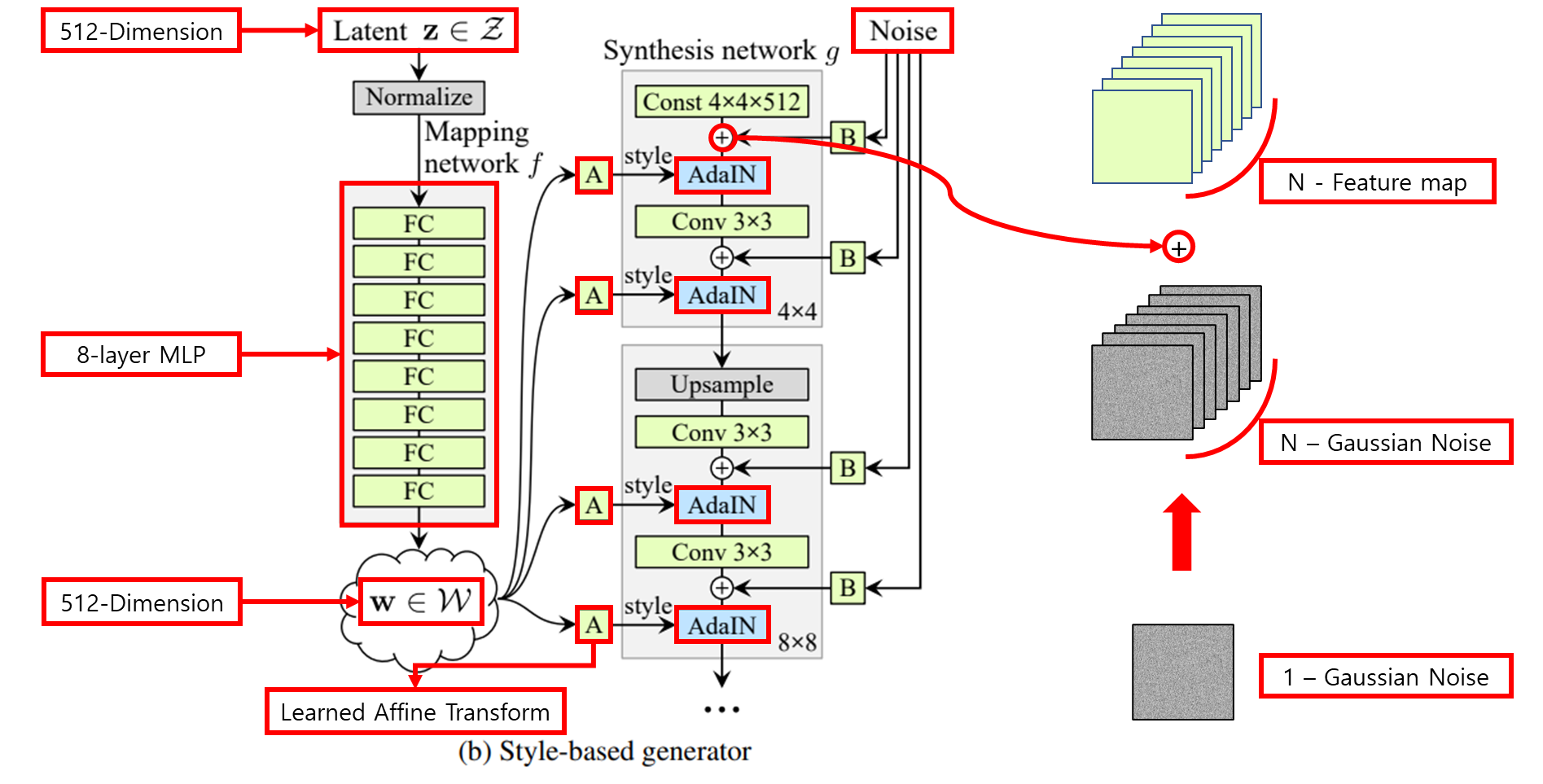
2.1 Non-linear mapping network

• 8-layer Multi Layer Perceptron(MLP)

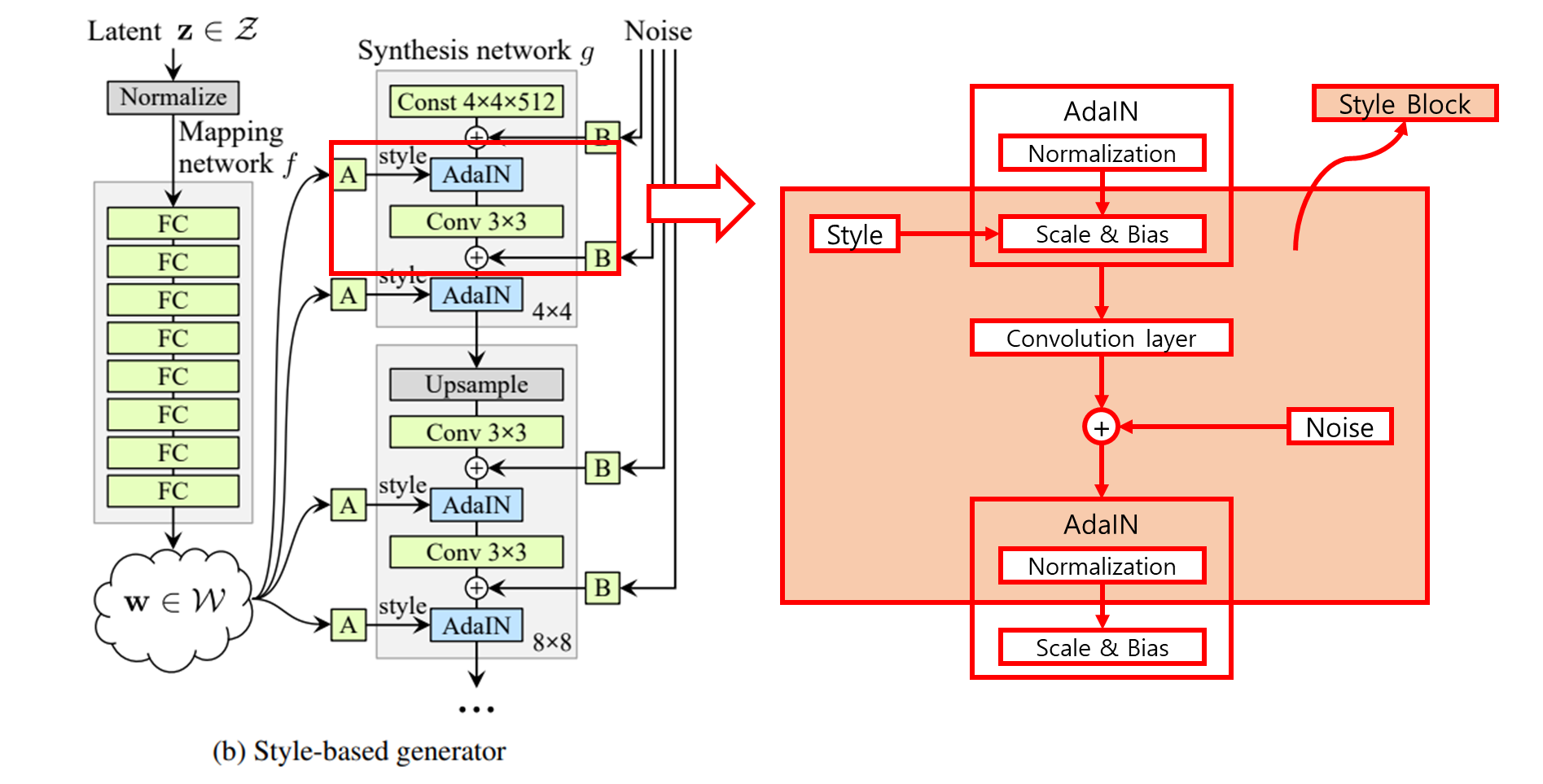
2.2 AdaIN(Adaptive Instance Normalization)

• $AdaIN(x, \ y) = \sigma(y)\left( \frac{x - \mu(x)}{\sigma(x)} \right) + \mu(y)$ → $x$ : 원하는 Contents를 담고 있는 feature map
  → $y$ : 원하는 Styles을 담고 있는 feature map
  → $\left( \frac{x - \mu(x)}{\sigma(x)} \right)$ : $x$에서 Styles을 빼고 남은 Contents
  → $\sigma(y)\left( \frac{x - \mu(x)}{\sigma(x)} \right) + \mu(y)$ : $x$에서 Styles을 빼고 남은 Contents에 $y$의 Styles을 추가

• 해당 paper에서 정의한 $AdaIN$

  • $AdaIN(x, \ y) = y_{s, i}\left( \frac{x_i - \mu(x_i)}{\sigma(x_i)} \right) + y_{b, i}$

• $AdaIN$을 사용한 이유

  • 일반적인 feature transform에 비해 간결하고 효율적이어서 사용했다.
    • Feature Transform → Standardization, Min-Max Scaling, Normalization…

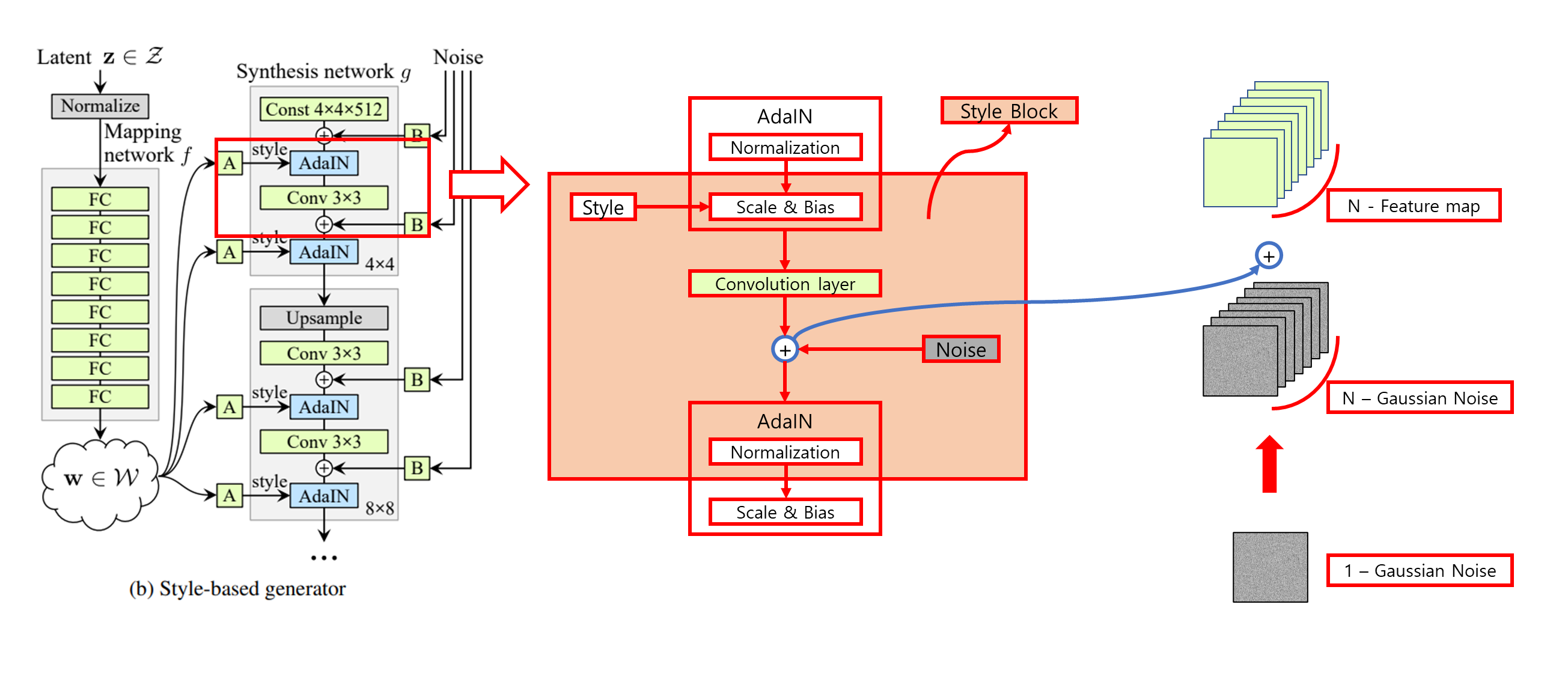
2.3 Noise

• Noise를 generator에 직접 넣어줌으로써 stochastic detail을 만들어냈다.

• Noise를 어떻게 generator(Synthesis network $g$)에 직접 넣을까?

  • Single channel로 이루어진 uncorrelated Gaussian noise를 convolution operation 이후 나오는 feature map의 갯수만큼 broadcasting 후 더해준다.

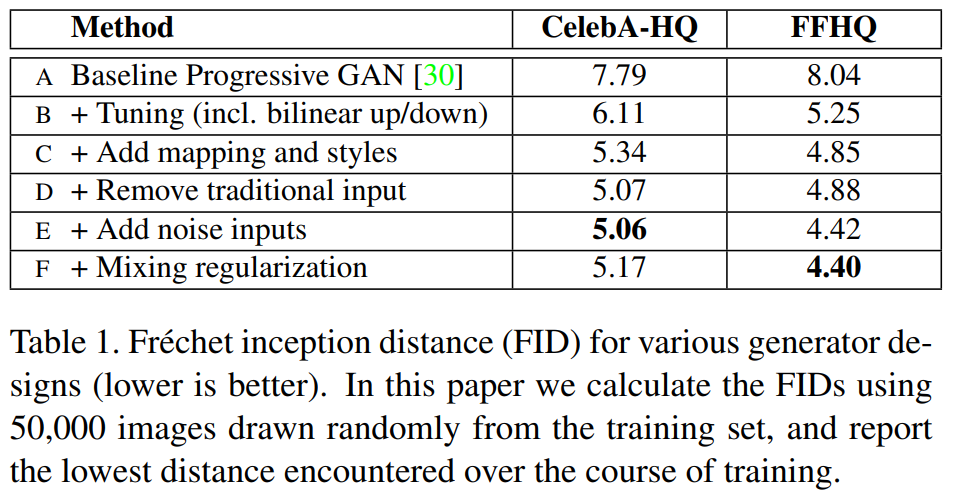
2.4 Quality of generated images

• 재설계된 Generator가 만드는 이미지의 품질이 향상됨을 입증

Method - A

• Progressive GAN을 그대로 가져와 FID를 측정

Method - B

• Progressive GAN에 bilinear upsampling, downsampling operation을 추가, 더 긴 훈련시간을 사용 그리고 hyperparameter를 조정하여 FID를 측정

Method - C

• Mapping network $f$와 $AdaIN$ operation을 추가하여 FID를 측정

Method - D

• Synthesis network $g$에 latent code를 input으로 하는 것이 더 이상 performance가 좋아지지 않음을 확인하고 기존의 latent code를 input으로하는 방식대신 학습된 4 x 4 x 512 상수를 input으로 하여 architecture를 단순화했다.

Method - E, F

• Method - E → Noise input

• Method - F → Style Mixing

• 생성된 이미지에 대해 세밀한 제어를 가능하게 했다.

---

3. Properties of the sylte-based generator

재설계한 generator의 특징들에 대하여 설명한다.

3.1 Style Localization

• Mapping network $f$와 affine transformation은 training dataset의 distribution으로부터 style을 학습하는 것으로 볼 수 있다.

• 여기서 style은 $AdaIN$ operation을 사용하여 localization 될 수 있다.

  • $AdaIN$ operation은 먼저 각 channel의 평균이 0이고 분산이 1이 되도록 normalize 한다.
  • 그 후, 다음 convolution operation이 적용되기 전 feature들의 중요성을 style에 관한 scale과 bias를 통해 조절한다.
  • 이때, normalization을 했기 때문에 $AdaIN$을 적용하기 전의 feature에는 영향을 받지 않는다.
  • 따라서 각 style은 $AdaIN$ operation이 적용되기 전 convolution layer만 제어한다.

• 이러한 style의 localization은 style을 scale별로 제어할 수 있음을 뜻한다.

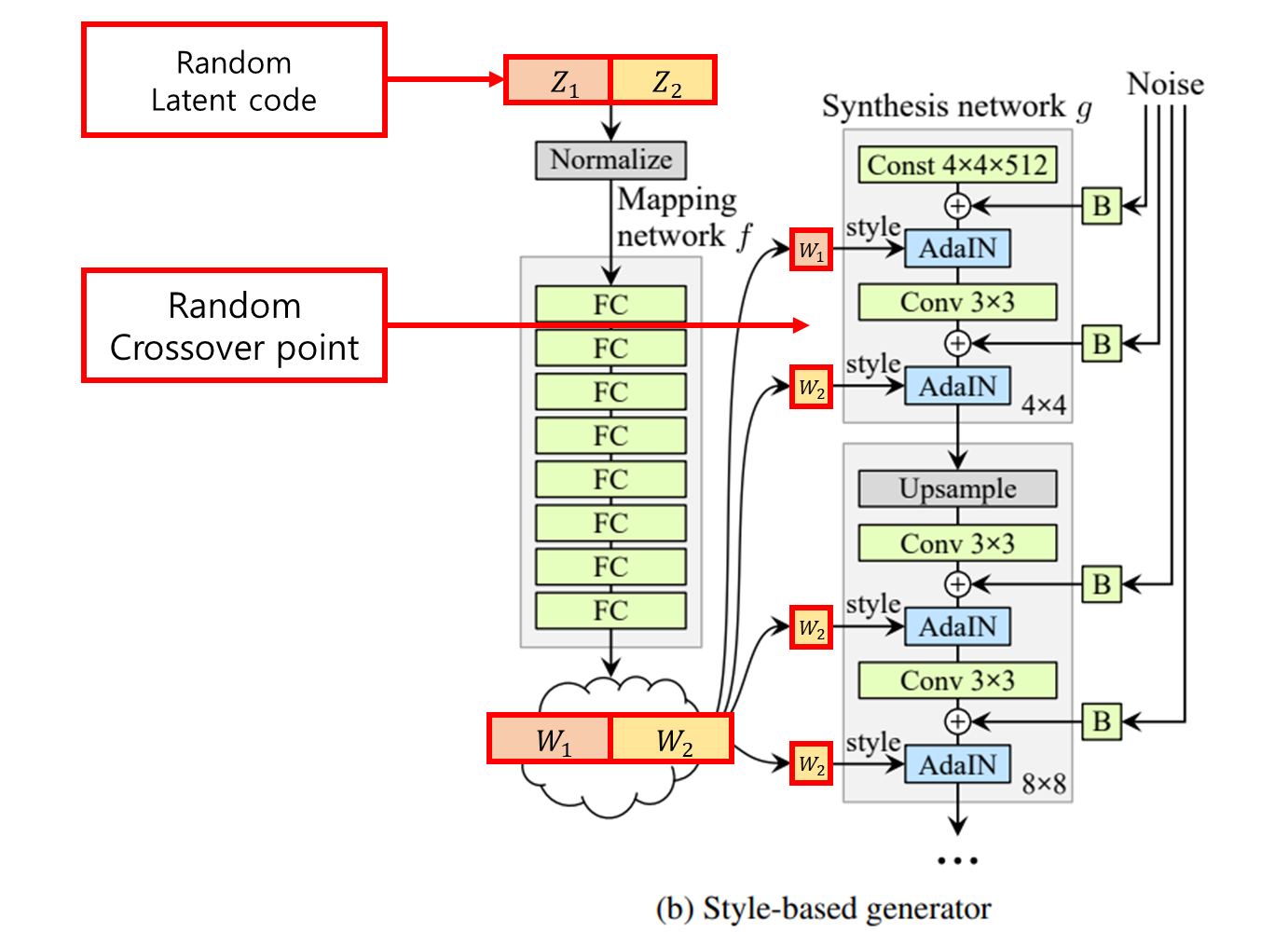
3.2 Style Mixing(Mixing regularization)

• Style의 localization이 잘 학습되도록 training동안 random으로 두 개의 latent code를 사용하여 이미지를 생성하는 mixing regularization을 사용했다.
  • Mixing regularization은 인접한 style의 correlation이 없도록 학습이 되게 한다.

• 무작위로 선택된 지점(crossover point)에서 하나의 latent code에서 다른 latent code로 switch하면 된다.

• Style Mixing을 다양한 scale에서 진행한 결과이다.

3.3 Stochastic variation

• Stochastic variation

  • 확률적으로 볼 수 있는 부분(머리카락, 수염, 주근깨, 피부 모공의 위치)이 올바른 distribution을 따른다면 머리카락, 수염, 주근깨, 피부 모공의 위치가 사람 얼굴이라고 판단하는데 영향을 주지 않으면서 무작위로 생성될 수 있다.

• Traditional generator가 stochastic variation을 구현하는 방법

  • Network로 들어오는 input이 input layer로 들어오는 input이 유일하기 때문에 network는 필요할 때마다 앞쪽 activation으로부터 spatially-varying pseudorandom number를 만들어내는 방법을 학습해야 한다.
    • pseudorandom number : 난수를 생성하기 위해 algorithm으로 생성된 값(Ex. seed를 통해 random number를 생성하는 것)
  • 이렇게 학습된 traditional generator가 만들어낸 stochastic image는 반복적인 패턴을 가진다.

• 재설계된 generator가 stochastic variation을 구현하는 방법

  • Single channel로 이루어진 uncorrelated Gaussian noise를 convolution operation 이후 나오는 feature map의 갯수만큼 broadcasting 후 더해준다.
  • 이러한 noise 추가는 확률적으로 볼 수 있는 부분에만 영향을 미쳤다.

• Noise Localization

  • Style localization과 비슷하게 noise는 noise가 들어간 style block의 weight들에만 영향을 미치도록 학습이 된다.
  • 따라서 noise의 효과가 localization 된다.

---

4. Disentanglement studies

• Mapping network $f$를 어떻게 학습시켜야 하는지 알 수 있었다.

4.1 Mapping network를 어떤 방향으로 학습을 시킬 것인가?

• Disentanglement

  • 각각의 variation factor로 제어되는 각각의 linear subspace로 구성된 latent space

• Latent z에서 각 factor의 조합의 sample이 추출될 확률은 training data의 분포와 상응하도록하여 latent z와 training set이 완전히 분리되는 것을 막는다.

• Latent w는 training data의 분포에서 sampling 할 필요가 없으므로 mapping network로부터 유도된다.

• Entangled representation을 기반으로 하는 것보다 disentangled representation을 기반으로 이미지를 생성하는 것이 더 쉽기 때문에 mapping network는 variation factor가 linear subspace를 구성하도록 학습이 된다.

4.2 Disentaglement를 측정하는 방법

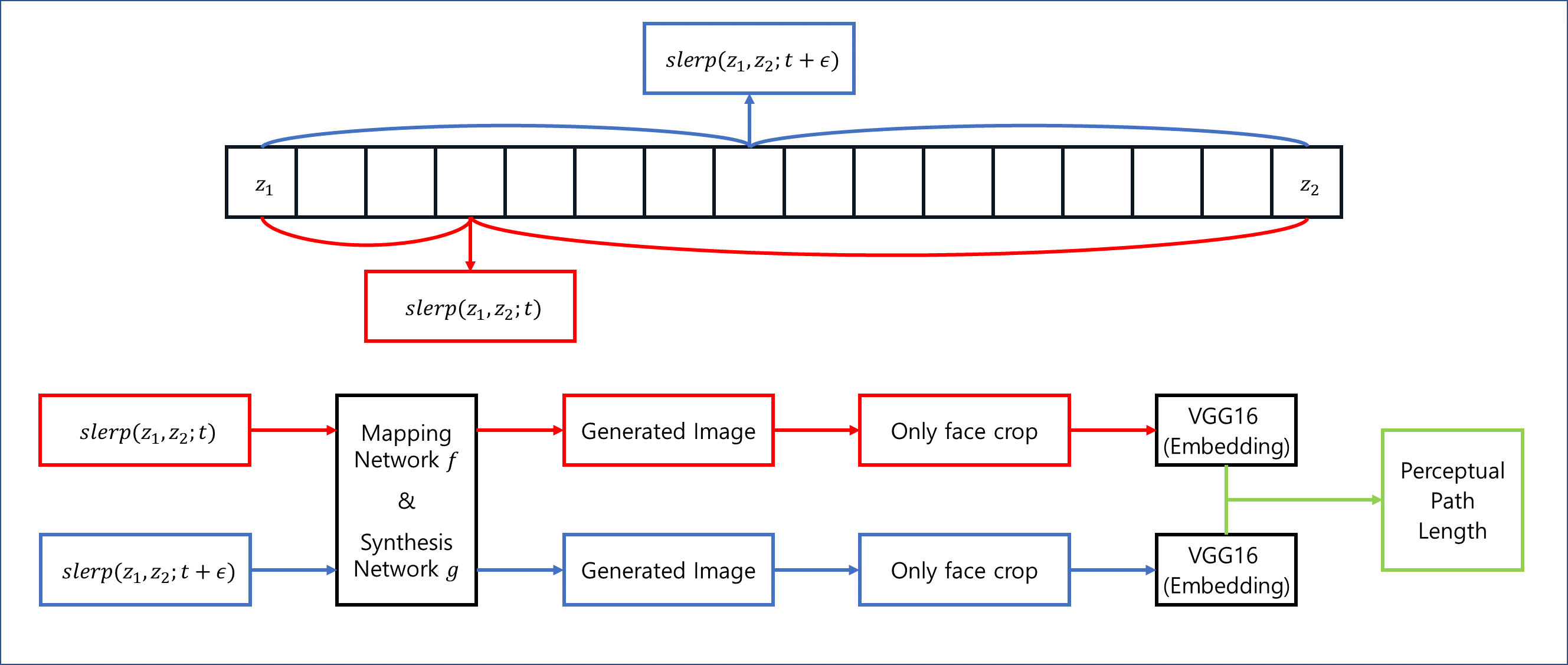
4.2.1 Perceptual path length

• Latent space가 entangle하다는 것은 variation factor가 제대로 분리되지 않았음을 뜻한다.

  • 이 경우 latent vector의 interpolation은 image에 놀랄 만큼 non-linear한 변화를 초래한다.
  • 따라서 latent space에서 interpolation을 수행할 때 얼마나 급격한 변화가 이미지에서 일어나는지 측정하여 entanglement를 정량화 할 수 있다.

• Perceptually-based pairwise image distance를 사용하여 측정

  • 두 개의 VGG16 model을 사용하여 차이를 계산

• SLERP

  • Normalized input latent space(latent z)에서 보간할 때 적절한 방법이다.

• LERP

  • Latent w에서 보간할 때 적절한 방법이다.
  • Mapping Network $f$를 지나지 않는 차이점이 있다.

4.2.2 Linear separability

• Latent space가 disentangle하다면 variation factor에 일관되게 대응하는 direction vector를 찾을 수 있어야 한다.

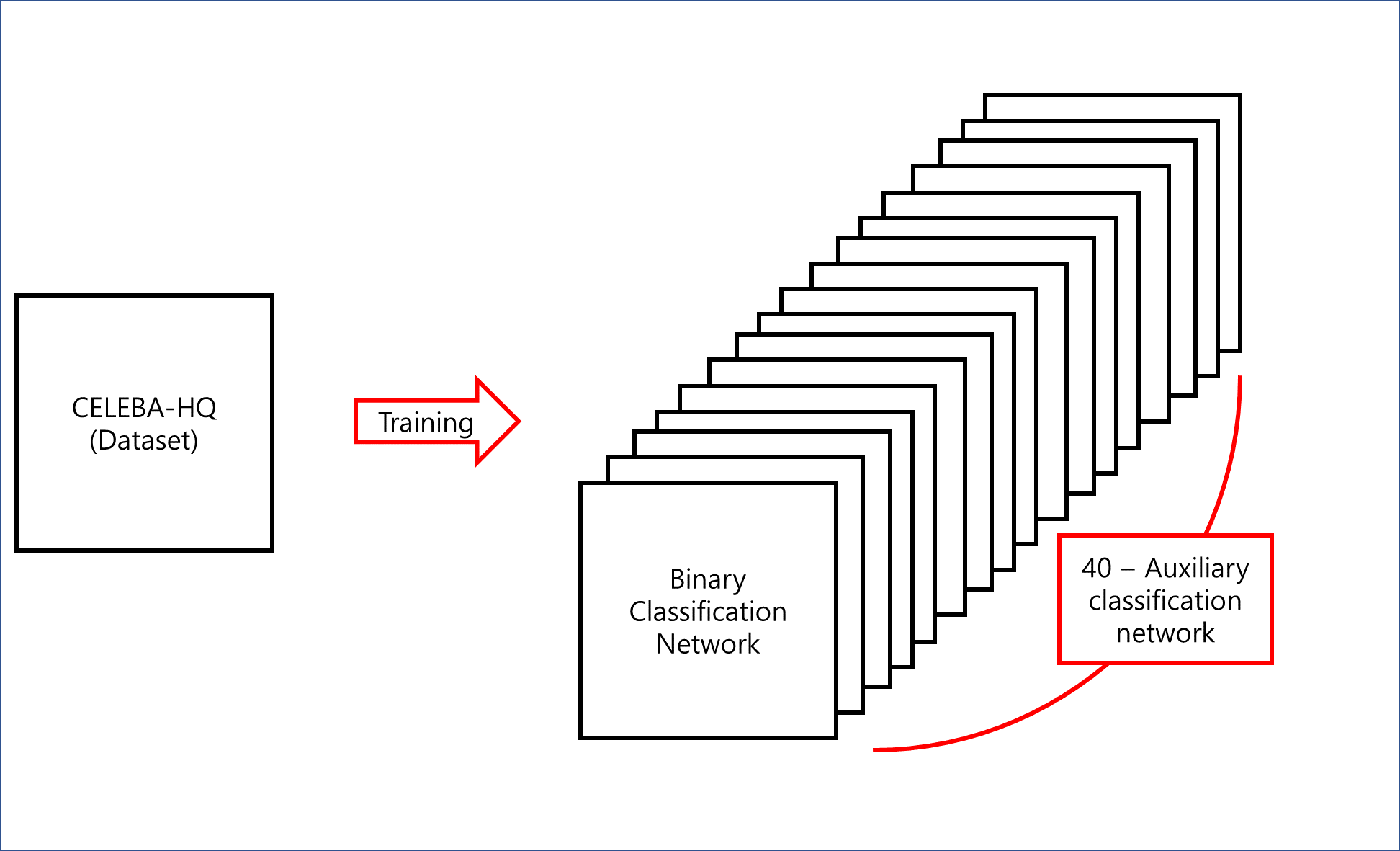
• Binary classification network를 훈련시킨다.

  • Network의 architecture는 discriminator와 동일한 architecture를 사용했다.
  • CELEBA-HQ dataset을 가지고 40개의 attributes를 학습

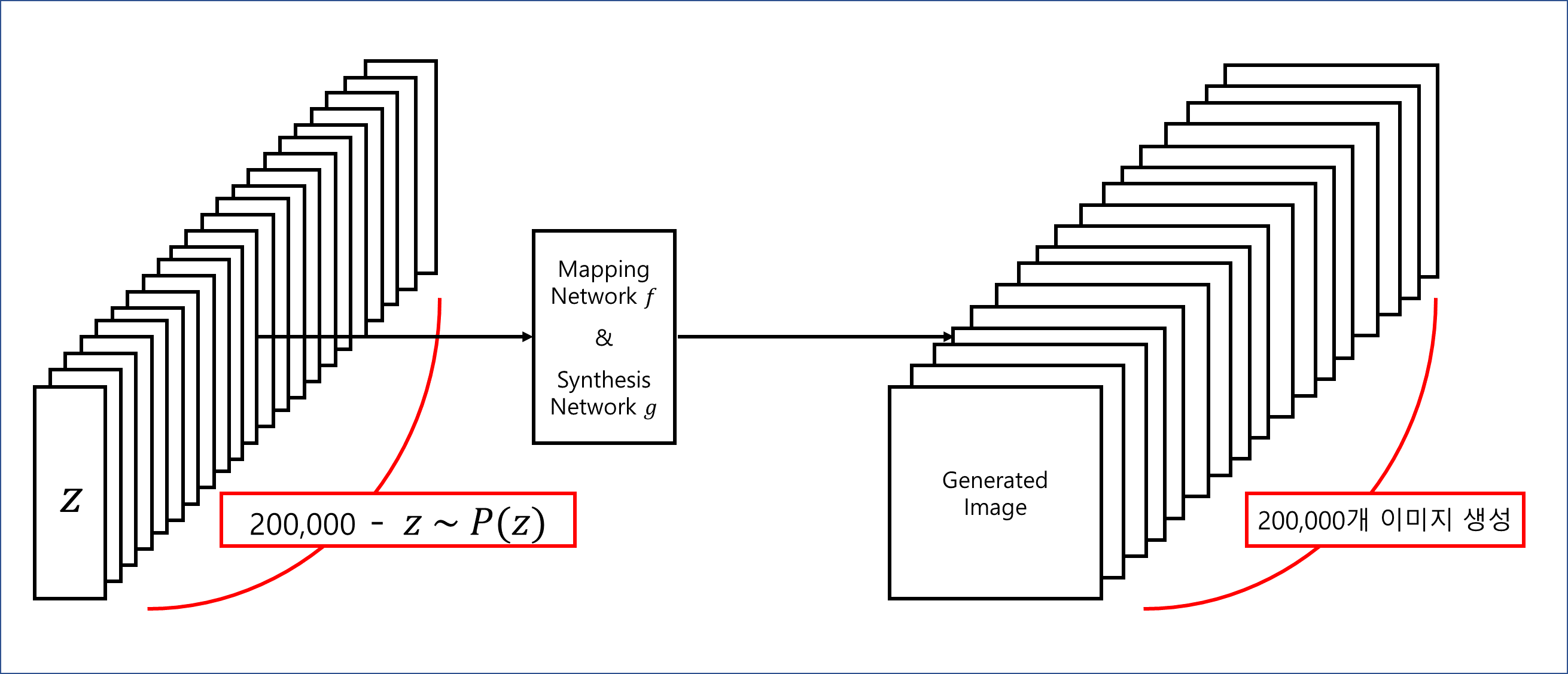
• 하나의 attribute의 separability를 측정하기 위해 $z \sim P(z)$로 200,000개의 이미지를 생성하고 binary classification network로 분류한다.

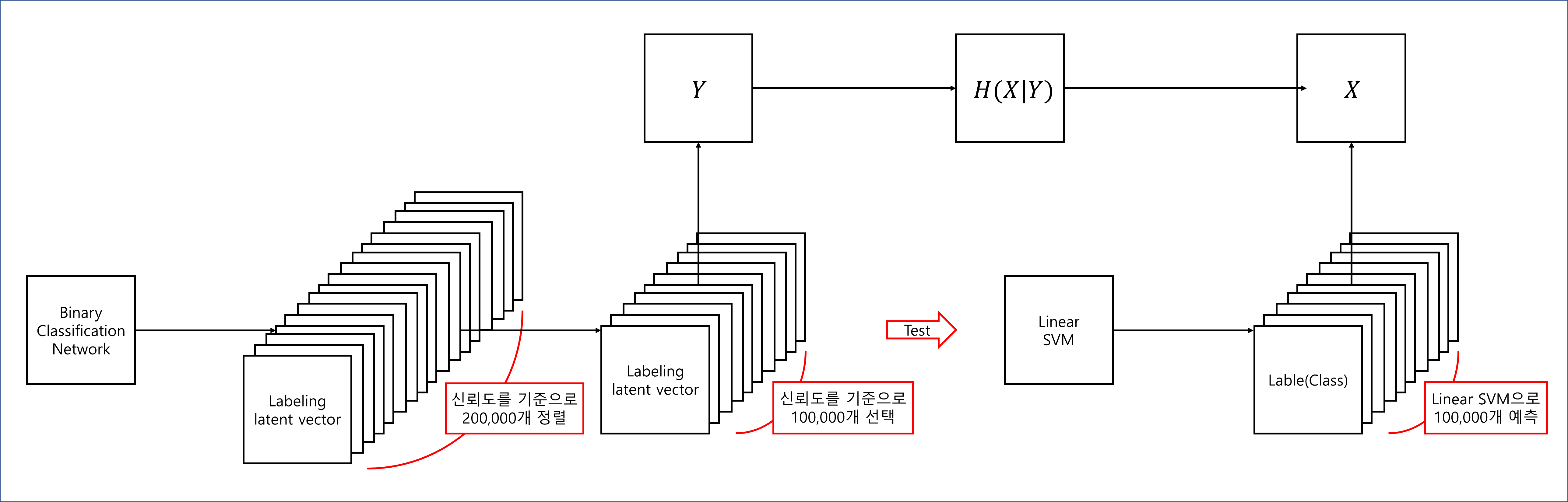
• 그런 다음 classifier의 신뢰도에 따라 sample을 정렬하고 신뢰도가 낮은 절반을 제거하여 100,000개의 labeling된 latent space vector를 만들어낸다.

• 각 attribute에 대해, 만들어진 latent vector를 linear SVM을 통해 class를 예측한다.

• Conditional entropy $H(Y\mid X)$
  • $H(Y\mid X)$는 어떤 확률변수 X가 다른 확률변수 Y의 값을 예측하는데 도움이 되는지를 측정하는 방법 중의 하나이다.
  • 만약 X가 어떤 특정한 하나의 값을 가질 때, Y도 마찬가지로 특정한 값이 된다면 X로 Y를 예측할 수 있으며 낮은 entropy 값을 가진다.
  • 반대로 X가 어떤 특정한 하나의 값을 가질 때, Y가 여러 값으로 골고루 분포되어 있다면 X는 Y를 예측하는데 도움이 안된다.
  • $X$ : linear SVM을 통해 예측된 class
  • $Y$ : Binary classification network에 의해 결정된 class
  • $H(Y\mid X)$의 낮은 값은 variation factor에 일관되게 대응하는 direction vector를 찾게 해준다.
• 40개의 attributes에 대해서 Final separability score를 계산
  • $exp(\Sigma_i H(Y_i\mid X_i))$